VSEPR-Modell
- Seiten mit Math-Fehlern
- Seiten mit Math-Renderingfehlern
- Seiten mit defekten Dateilinks
- Physikalische Chemie
- Chemische Bindung
- Isomerie
Das VSEPR-Modell (VSEPR ist die Abkürzung für englisch valence shell electron pair repulsion, deutsch Valenzschalen-Elektronenpaar-Abstoßung), auch EPA-Modell (Elektronenpaarabstoßungsmodell) oder ursprünglich auch VEPR-Theorie (englisch valence electron pair repulsion theory), führt die räumliche Gestalt eines Moleküls auf die abstoßenden Kräfte zwischen den Elektronenpaaren der Valenzschale zurück.
Das Modell wurde von Ronald Gillespie und Ronald Nyholm entwickelt und wird deshalb auch Gillespie-Nyholm-Theorie genannt.
Die abgeleiteten Regeln
Aus dem VSEPR-Modell ergeben sich für Moleküle des Typs AXn folgende Regeln[1]:
- Die Elektronenpaare des Zentralatoms (A), das heißt das Atom im Zentrum des Moleküls, ordnen sich so an, dass der Abstand zwischen ihnen möglichst groß wird.
- Die freien Elektronenpaare (hier mit E symbolisiert) in einem Molekül vom Typ AXnEm beanspruchen mehr Raum als die bindenden Elektronenpaare und führen somit zu einer Vergrößerung der Winkel X-A-E und einer Verkleinerung der Winkel X-A-X.
- Größere Elektronegativitätsdifferenzen zwischen A und X vermindern damit den Raumbedarf der entsprechenden Bindung.
- Mehrfachbindungen beanspruchen mehr Raum als Einfachbindungen. Hierbei steigt der Platzbedarf mit der Bindungsordnung. Einzelne freie Elektronen in Radikalen nehmen hingegen weniger Raum ein als freie Elektronenpaare. Für die Bestimmung der groben Molekülstruktur werden jedoch nur die Sigma-Bindungen herangezogen. Das heißt, dass Mehrfachbindungen bei der Bestimmung der Struktur wie Einfachbindungen behandelt werden.
- Kleinere Zentralatome bzw. größere negativ polarisierte Liganden bewirken eine starke sterische und elektronische Abstoßungskraft, die die eines freien Elektronenpaars übertreffen kann.
Vorhersagen nach VSEPR bei freien Elektronenpaaren am Zentralatom
Molekülstrukturen können recht einfach durch Abzählen der „Reste“ vorhergesagt werden, wenn keine freien Elektronenpaare am Zentralatom vorhanden sind. Dennoch lässt sich auch die näherungsweise Betrachtung von Verbindungen mit einem oder mehreren freien Elektronenpaaren schematisieren, indem freie Elektronenpaare wie Bindungspartner behandelt werden: Man gelangt hierüber zur Pseudostruktur(Ψ - Struktur, von Ψ, der Wellenfunktion der Elektronen) des jeweiligen Moleküls.
Das Sauerstoffatom des Wassermoleküls, an welches zwei Wasserstoffatome kovalent geknüpft sind, weist zwei freie Elektronenpaare auf. Dementsprechend ergibt sich aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): X = 2 (Wasserstoffatome) und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): E = 2 (freie Elektronenpaare) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): 2+2=4 und somit eine tetraedrische Geometrie. Die Molekülgestalt selbst wird aber nur durch die Atomkerne beschrieben. Indem die freien Elektronenpaare nun „weggedacht“ werden, bleibt die Realstruktur zurück: gewinkelt.
| # | Molekültypen * | Beispiel | Ψ - Struktur ** | Realstruktur *** | Winkel |
|---|---|---|---|---|---|
| 1 | Datei:AX1E0-2D.png AX1 |
H2 | Datei:AX1E0-3D-balls.png linear |
Datei:AX1E0-3D-balls.png linear |
180° |
| 2 | Datei:AX2E0-2D.png AX2 |
BeCl2 CO2 |
Datei:AX2E0-3D-balls.png linear |
Datei:Linear-3D-balls.png linear |
180° |
| Datei:AX1E1-2D.png AX1E1 |
Datei:AX1E1-3D-balls.png linear |
Datei:AX1E0-3D-balls.png linear |
180° | ||
| 3 | Datei:AX3E0-side-2D.png AX3 |
BF3 NO3− CO32− |
Datei:AX3E0-3D-balls.png trigonal planar |
Datei:Trigonal-3D-balls.png trigonal planar |
120° |
| Datei:AX2E1-2D.png AX2E |
SO2 O3 NO2− |
Datei:AX2E1-3D-balls.png trigonal planar |
Datei:Bent-3D-balls.png gewinkelt |
ca. 115° | |
| Datei:AX1E2-2D.png AX1E2 |
Datei:AX1E2-3D-balls.png trigonal planar |
Datei:AX1E0-3D-balls.png linear |
180° | ||
| 4 | Datei:AX4E0-2D.png AX4 |
CH4 SO42− PO43− ClO4− |
Datei:AX4E0-3D-balls.png tetraedrisch |
Datei:Tetrahedral-3D-balls.png tetraedrisch |
109,5° |
| Datei:AX3E1-2D.png AX3E |
NH3 PCl3 |
Datei:AX3E1-3D-balls.png tetraedrisch |
Datei:Pyramidal-3D-balls.png trigonal-pyramidal |
ca. 107° | |
| Datei:AX2E2-2D.png AX2E2 |
H2O | Datei:AX2E2-3D-balls.png tetraedrisch |
Datei:Bent-3D-balls.png gewinkelt |
ca. 104° | |
 AX1E3 |
HCl | Datei:AX1E3-3D-balls.png tetraedrisch |
Datei:AX1E0-3D-balls.png linear |
180° | |
| 5 | Datei:AX5E0-2D.png AX5 |
PCl5 | Datei:Trigonal-bipyramidal-3D-balls.png trigonal-bipyramidal |
Datei:Trigonal-bipyramidal-3D-balls.png trigonal-bipyramidal |
120° / 90° |
| Datei:AX4E1-2D.png AX4E |
SF4 | Datei:AX4E1-3D-balls.png trigonal-bipyramidal |
Datei:Seesaw-3D-balls.png "Wippe", bisphenoidal |
ca. 175° / 110° | |
| Datei:AX3E2-2D.png AX3E2 |
ClF3 | Datei:AX3E2-3D-balls.png trigonal-bipyramidal |
Datei:T-shaped-3D-balls.png T-förmig |
ca. 87,5° | |
| Datei:AX2E3-2D.png AX2E3 |
XeF2 | Datei:AX2E3-3D-balls.png trigonal-bipyramidal |
Datei:Linear-3D-balls.png linear |
180° | |
| 6 | Datei:AX6E0-2D.png AX6 |
SF6 | Datei:AX6E0-3D-balls.png oktaedrisch (=quadratisch-bipyramidal, trigonal-antiprismatisch) |
Datei:Octahedral-3D-balls.png oktaedrisch (=quadratisch-bipyramidal, trigonal-antiprismatisch) |
90° |
 AX5E |
ClF5 | 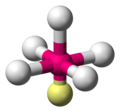 oktaedrisch (=quadratisch-bipyramidal, trigonal-antiprismatisch) |
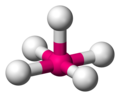 quadratisch-pyramidal |
ca. 85° | |
 AX4E2 |
XeF4 |  oktaedrisch (=quadratisch-bipyramidal, trigonal-antiprismatisch) |
Datei:Square-planar-3D-balls.png quadratisch-planar |
90° | |
| 7 |  AX7 |
IF7 |  pentagonal-bipyramidal |
 pentagonal-bipyramidal |
90° / 72° |
 AX6E |
XeF6 | 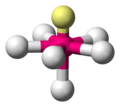 pentagonal-bipyramidal |
pentagonal-pyramidal |
ca. 90° / ca. 72° | |
| AX5E2 | XeF5− | pentagonal-bipyramidal | pentagonal-planar |
72° | |
| 8 | AX8 | IF8− | tetragonal-antiprismatisch | tetragonal-antiprismatisch | 78° / 73° |
Anmerkungen:
Grenzen der Anwendbarkeit
Das VSEPR-Modell lässt sich auf Moleküle anwenden, bei denen die an das Zentralatom gebundenen Reste (Atome oder Atomgruppen) nicht allzu groß werden und keine spezifischen Wechselwirkungen aufeinander ausüben. Nicht oder nur eingeschränkt anwendbar ist sie auf Übergangsmetallverbindungen. Vielfach fallen auch schon bei einfachen Molekülen Valenzwinkel aus dem Rahmen, die nicht mit dem Modell übereinstimmen. Für Verbindungen mit delokalisierten Elektronen ist die Anwendung des Modells ebenfalls mit Schwierigkeiten verbunden, hier ist die Hinzuziehung der Molekülorbitaltheorie notwendig.
Literatur
- Reinhart Ahlrichs: Gillespie‐ und Pauling‐Modell — ein Vergleich. In: Chemie in unserer Zeit. 14, Nr. 1, 1980, S. 18–24, doi:10.1002/ciuz.19800140104.
- Ronald J. Gillespie, Edward A. Robinson: Models of molecular geometry. In: Chemical Society Reviews. 34, Nr. 5, 2005, S. 396–407, doi:10.1039/B405359C.
- R. J. Gillespie, I. Hargittai: The VSEPR Model of Molecular Geometry. 8. Aufl., Allyn & Bacon, Boston 1991, ISBN 978-0-205-12369-8.
Weblinks
Einzelnachweise
- ↑ Arnold Fr. Holleman, Egon Wiberg: Lehrbuch der Anorganischen Chemie. 101. Auflage. Gruyter, 1995, ISBN 3-11-012641-9, S. 136 und 315.