Arbeit (Physik)
- Seiten mit defekten Dateilinks
- Physikalische Größe
Arbeit ist ein Begriff der Klassischen Mechanik. Zur Abgrenzung von anderen Definitionen von Arbeit spricht man hier auch von mechanischer Arbeit.
Arbeit (Formelzeichen $ W $ von englisch work) wird verrichtet, wenn eine Kraft längs eines Weges auf einen Körper wirkt. Arbeit ist im einfachsten Fall das Produkt aus der in Wegrichtung wirkenden Kraft und der Wegstrecke, bei nicht geradlinigen Wegen das Kurvenintegral über das Skalarprodukt aus Kraft und Weg.
Arbeit ist mechanisch übertragene Energie – in diesem Zusammenhang spricht man auch von Energie als gespeicherter Arbeit bzw. Energie als der Fähigkeit, Arbeit zu verrichten.
Die SI-Einheit der Arbeit ist das Joule (Einheitenzeichen J). Aus dem Bezug der Arbeit zur Kraft (SI-Einheit Newton) und Leistung (SI-Einheit Watt) ergeben sich die abgeleiteten SI-Einheiten Newtonmeter (Nm) und Wattsekunde (Ws). Es gilt 1 J = 1 Nm = 1 Ws. Häufig werden auch die Einheiten Wattstunde (Wh) bzw. Kilowattstunde (kWh) verwendet.
Mit spezifischer Arbeit (Formelzeichen $ w $) ist in der Thermodynamik das auf die Masse des Strömungsfluides bezogene Arbeitsvermögen, Einheit J/kg, gemeint (siehe auch Totalenthalpie).
Definition
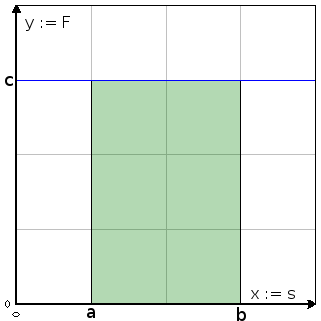
In der Physik ist Arbeit das Skalarprodukt aus Kraft und Weg: Wenn auf einen Körper auf der geraden Strecke vom Punkt A zum Punkt B eine konstante Kraft $ {\vec {F}} $ wirkt, dann wird am Körper die Arbeit
- $ W={\vec {F}}\cdot {\vec {s}}=|{\vec {F}}|\,|{\vec {s}}|\,\cos \sphericalangle \left({\vec {F}},{\vec {s}}\right)\, $
verrichtet. Dabei ist $ {\vec {s}} $ der Vektor von A nach B, und sein Skalarprodukt mit dem Vektor $ {\vec {F}} $ ist das Produkt der Beträge $ |{\vec {F}}| $ und $ |{\vec {s}}| $ mal dem Kosinus des eingeschlossenen Winkels.
Die Bedeutung des physikalischen Begriffs Arbeit beruht auf folgendem Sachverhalt: Beschleunigt die betrachtete Kraft die Bewegung des Körpers, so erhöht sich seine kinetische Energie auf dem Weg von A nach B um die an ihm verrichtete Arbeit.
Wirkt die konstante Kraft in Richtung des zurückgelegten Weges, dann ist die Arbeit das Produkt der Beträge $ W=|{\vec {F}}|\,|{\vec {s}}|\, $, da der Winkel null und sein Kosinus = 1 ist.
Ist die Richtung der Kraft der Bewegungsrichtung entgegengesetzt, dann bilden die beiden Vektoren einen Winkel von 180°, dessen Kosinus der Wert -1 ist. In diesem Fall wird an dem Körper eine negative Arbeit verrichtet, die Kraft wirkt als Bremskraft.
Ist die Richtung der Kraft senkrecht zum Weg, dann wird keine physikalische Arbeit verrichtet. Der physikalische Begriff entspricht also nicht dem alltäglichen Verständnis, nach dem jeder Kofferträger für seine verrichtete Arbeit bezahlt wird.
Wenn die Kraft nicht entlang des gesamten Weges konstant ist oder der Weg nicht gerade ist, so kann man die Arbeit näherungsweise berechnen, indem man den Weg durch einen Streckenzug aus N geraden Teilstücken $ \Delta {\vec {s}}_{i} $ nähert, auf denen die Kraft $ {\vec {F}}(s_{i}) $ jeweils näherungsweise als konstant angenommen werden kann. Die entlang des gesamten Weges verrichtete Arbeit ergibt sich dann näherungsweise durch Aufsummierung der Arbeiten entlang der einzelnen Wegstücke als
- $ W\approx \sum _{i=1}^{N}W_{i}=\sum _{i=1}^{N}{\vec {F}}(\mathbf {s} _{i})\cdot \Delta {\vec {s}}_{i}\,. $
Um den genauen Wert zu erhalten, wählt man die Wegstücke immer kleiner, so dass ihre Länge gegen Null und ihre Anzahl gegen unendlich geht. Der Grenzwert der Summe ist das Weg- oder Kurvenintegral
- $ W=\int _{\mathbf {s} _{1}}^{\mathbf {s} _{2}}{\vec {F}}(\mathbf {s} )\cdot \mathrm {d} {\vec {s}}\,, $
wobei $ \mathbf {s} _{1}\, $ den Anfangs- und $ \mathbf {s} _{2}\, $ den Endpunkt des Weges bezeichnen.
In einem konservativen Kraftfeld ist die so berechnete Arbeit vom Weg unabhängig und hängt nur vom Anfangs- und Endpunkt ab. Daher ist die Arbeit entlang eines geschlossenen Weges (Anfangspunkt gleich Endpunkt) in einem konservativen Kraftfeld gleich Null.
Beispiele
- Hubarbeit: Arbeit, die an einem ruhenden Körper der Masse $ m $ verrichtet werden muss, um ihn im homogenen Schwerefeld mit Gravitationsbeschleunigung $ g $ um die Hubhöhe $ h $ zu heben
- $ W(h)=F_{g}\,h=m\,g\,h\,. $
- Die Hubarbeit ist der Unterschied der potentiellen Energie an Ziel und Start.
- Beispiel: $ m=1\,\mathrm {kg} ,g=9{,}81\,\mathrm {m} /\mathrm {s^{2}} ,F_{g}=m\,g=9{,}81\,\mathrm {N} ,h=40\,\mathrm {cm} ,W(h)=9{,}81\,\mathrm {N} \cdot 0{,}4\,\mathrm {m} \approx 4\,\mathrm {J} \,. $
- Spannarbeit
- Siehe auch: Federarbeit
- $ W_{\mathrm {sp} }=\int _{s_{1}}^{s_{2}}D\,y\,\mathrm {d} y={\frac {D}{2}}\left(s_{2}^{2}-s_{1}^{2}\right)\,, $
- wobei $ D $ die Federkonstante und $ F=-D\,y $ die Federkraft ist. Gegen diese Kraft muss Arbeit am angehängten Pendelkörper verrichtet werden, um ihn von Auslenkung $ s_{1} $ zur Auslenkung $ s_{2} $ (von anfänglicher Ruhe zu schließlicher Ruhe) zu bewegen. Das Koordinatensystem ist so gewählt, dass in der Ruhelage $ y=0 $ gilt.
- Die Spannarbeit zählt wie die Volumenarbeit zu Arbeit, die bei Verformungen verrichtet werden muss.
- Beschleunigungsarbeit, siehe etwa Schwungradspeicherung
- elektrische Arbeit
Siehe auch
- Potential (Physik)
Literatur
- Bärbel Grimm u. A.: Das neue Tafelwerk - Sekundarstufe. Volk und Wissenverlag, 1995, ISBN 3-06-000726-8
- Christian Gerthsen, Dieter Meschede, Helmut Vogel (Herausgeber bis zur 20. Auflage): Physik, 23. Auflage, Springer Verlag, Berlin 2006, ISBN 3-540-25421-8, E-Book 9783540299738