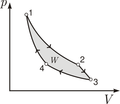
Polytrop

In der Thermodynamik wird eine Zustandsänderung eines Systems, in der für Druck p und Volumen V die Gleichung $ pV^{n}=\mathrm {const} $ gilt, als polytrop bezeichnet. Der Exponent $ n $ wird Polytropenexponent genannt. Sonderfälle der polytropen Zustandsänderung sind:

Spezialfälle der polytropen Zustandsänderung

• n = 0 : isobar
• n = 1 : isotherm
• n → ∞ : isochor
• n = $ \ \kappa ={\frac {c_{p}}{c_{V}}} $ : isentrop oder auch adiabat-reversibel

Die einem Gas während dieser Zustandsänderung zugeführte Wärme ist gegeben durch ^[1]:

$ Q_{12}=m\ c_{v}{\frac {n-\kappa }{n-1}}\ (T_{2}-T_{1}) $

Dabei bezeichnet m die Masse, T₁ und T₂ Anfangs- und Endtemperatur des Prozesses. Die Polytropie zeichnet sich durch eine feste Wärmekapazität aus, welche sich aus c_p, c_v und n ergibt.

Literatur

• Dieter Winklmair - Energie- und Wärmetechnik (Skript, PDF) (1,08 MB)

Einzelnachweise

Siehe auch

Wiktionary: polytrop – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Thermische Zustandsgleichung idealer Gase

Thermodynamische Zustandsänderungen

adiabatisch | diabatisch · isenthalp · polytrop: isobar | isochor | isotherm | isentrop