Nachzerfallswärme

Nachzerfallswärme als Anteil der Nennleistung nach Schnellabschaltung, berechnet nach zwei verschiedenen Modellen: Retran^[1] ohne Berücksichtigung eines vorherigen Betriebs und Todreas^[2] unter Annahme von 2 Jahren Betrieb vor Abschaltung.

Mit Nachzerfallswärme (englisch decay heat) bezeichnet man in der Kernreaktor-Technik die Zerfallswärmeleistung, die nach dem Beenden der Kettenreaktion in den Brennelementen noch neu entsteht. Da der Neutronenfluss z. B. durch Einfahren der Steuerstäbe nahezu zum Erliegen gekommen ist, finden nach der Abschaltung kaum neue Spaltungsreaktionen statt. Die Nachzerfallswärme kommt vielmehr dadurch zustande, dass die vorhandenen, kurzlebigen Spaltprodukte radioaktiv zerfallen.

Die Wärmemenge und der Dampfdruck reichen nach dem Abschalten im Allgemeinen nicht mehr für den Betrieb der Dampfturbine aus. Die Nachzerfallswärme muss daher komplett über den normalen oder einen speziellen Kühlkreislauf abgeführt werden. Diese Wärmeleistung beträgt unmittelbar nach dem Abschalten zwischen 5 % und 10 % der vorherigen thermischen Leistung des Reaktors; abhängig vom Reaktortyp, der Betriebsdauer und dem eingesetzten Kernbrennstoff. In einem Großreaktor von beispielsweise 1.300 Megawatt elektrischer Leistung, d. h. rund 4.000 MW thermischer Leistung,^{[Anm. 1]} entstehen somit direkt nach der Abschaltung noch rund 200 bis 400 MW Wärmeleistung, die danach relativ schnell abfällt.

Durch die Nachzerfallswärme können bei vollständigem Ausfall der Kühlung Schäden am Reaktor bis hin zur Kernschmelze eintreten. Deshalb benötigen auch Leichtwasserreaktoren geeignete Notkühlsysteme.

Umgangssprachlich wird auch der Begriff Restwärme gebraucht. Dieser ist aber irreführend, da die Nachzerfallswärme nicht die gespeicherte Wärmemenge des Reaktorkerns (Wärmekapazität) beim Abschalten beschreibt, sondern die Leistungserzeugung der andauernden radioaktiven Zerfälle.

Berechnung

Für jedes einzelne Radionuklid klingt die Nachzerfallswärmeleistung entsprechend einer Exponentialfunktion ab. Bei dem Spaltproduktgemisch in einem Reaktor überlagern sich die Exponentialfunktionen zu einem Verlauf, der für praktische Zwecke nach Näherungsformeln berechnet werden kann. Die Berechnungsvorschriften sind in den Normen DIN 25463-1 und DIN 25463-2 festgelegt.

Eine Näherungsformel für die Abnahme der Wärmemenge wurde 1946 von Way und Wigner angegeben.^[3] Wird ein Reaktor für die Dauer $T_{0}$ mit der Leistung $P_{0}$ betrieben, so ist die Nachzerfallsleistung $P$ zum Zeitpunkt $t$ nach dem Abschalten des Reaktors

P (t) = P_{0} \cdot 6, 22 \cdot 10^{- 2} \cdot (t^{- 0, 2} - {(T_{0} + t)}^{- 0, 2}) .

Dabei sind T₀ und t in Sekunden einzusetzen. Die Formel gilt (bei einer hinreichend langen Betriebsdauer T₀) für den Zeitraum etwa 10 Sekunden bis etwa 100 Tage nach der Abschaltung. Aus dem Artikel von Way & Wigner (1946 bzw. 1948) ist ersichtlich, wie die mittlere Nachzerfallsleistung der Produkte eines Spaltereignisses mit Hilfe der Bethe-Weizsäcker-Formel (Liquid-Drop-Modell zur Berechnung der Energiedifferenzen der Zerfallsprodukte in der radioaktiven Zerfallskette) und der Sargent-Regel (mittlere Lebensdauer eines $β$ -Strahlers ist näherungsweise invers proportional zur fünften Potenz der Energiedifferenz von Mutter- und Tochterkern, die auch in Verbindung zur maximalen Elektronenenergie gebracht werden kann) berechnet werden kann. Man erhält ein Abklingen dieser Einzelnachzerfallsleistung wie $t^{- 1, 2}$ , wenn der Zerfall zur Zeit $t = 0$ stattfand. D.h. wenn der Zerfall zur Zeit $t^{'}$ stattgefunden hat, erhält man

P_{1} (t - t^{'}) \propto (t - t^{'})^{- 1, 2} .

Unter der Annahme, dass ${\dot{N}}_{0}$ Kerne gleichverteilt über ein Intervall $[- T_{0}, 0]$ gespalten wurden, so erhält man die gesamte Nachzerfallsleistung durch Integration

P (t) = {\dot{N}}_{0} \int_{- T_{0}}^{0} P_{1} (t - t^{'}) d t^{'} \propto {\dot{N}}_{0} \int_{- T_{0}}^{0} (t - t^{'})^{- 1, 2} d t^{'} = {\dot{N}}_{0} (t^{- 0, 2} - (T_{0} + t)^{- 0, 2}) .

Da die Anzahl der gespaltenen Kerne pro Sekunde, ${\dot{N}}_{0}$ mit der Leistung des Reaktors in Verbindung gesetzt werden kann (unter der Annahme zeitlicher konstanter Leistung), d.h.

P_{0} = ⟨ E_{s} ⟩ \cdot {\dot{N}}_{0},

wobei $⟨ E_{s} ⟩$ die mittlere Energie, die pro Spaltung thermisch nutzbar ist (etwa 200 MeV pro Spaltung), so kann man die Nachzerfallsleistung auch auf die gefahrene Reaktorleistung beziehen, wie oben angegeben. Der korrekte Vorfaktor ergibt sich demnach aus der korrekten mittleren Einzelnachzerfallsleistung und der mittleren, pro Spaltung thermisch nutzbaren Energie.

Die Herleitung von Way und Wigner beruht auf sehr groben Modellannahmen, die im Einzelnen durchaus nicht zutreffen müssen. Daher gehen sie selbst von einem Fehler im Bereich von 15 % bis 20 % aus. Beispielsweise folgen nicht alle $β$ -instabilen Nuklide der Sargent-Regel. Es gibt bestimmte erlaubte und nicht-erlaubt Übergänge, die sich stark auf die Lebensdauer eines $β$ -Strahlers auswirken können. Die Massenzahlen, $A_{L}$ und $A_{H}$ , der Spaltprodukte wurden in der Ableitung bei den Maxima fixiert (in Wirklichkeit sind sie charakteristisch verteilt mit zwei Maxima; siehe Spaltprodukt). Auch ist eine Zuordnung für eine gegebene Massenzahl $A$ zu einer festen Protonenzahl $Z$ nicht eindeutig bei den Spaltprodukten, so dass hier (jeweils für die leichten (L) und schweren (H) Spaltprodukte) eine Gauß-Verteilung für $Z$ um einen Mittelwert angenommen wurde. Hier kommen die 15 % bis 20 % Ungenauigkeit her. Schließlich haben Way und Wigner die gesamte Nachzerfallsleistung bestimmt, inklusive $γ$ -Zerfälle und kinetische Energie der Neutrinos. Um die eigentliche thermische Nachzerfallsleistung daraus zu bestimmen, sind ein paar Annahmen nötig über die Verteilung der Zerfallsenergie auf Elektronen, Neutrinos und Photonen. Es ist erstaunlich, dass im Mittel die theoretische Voraussage dieses Modellansatzes mit experimentellen Ergebnissen so gut übereinstimmt (den Angaben der Autoren zufolge).

Schließlich wurde bei der obigen Integration völlig außer Acht gelassen, dass bestimmte Nuklide durch Neutroneneinfang aus der Zerfallskette teilweise entfallen, d.h. inaktiv werden können oder ihr weiterer Zerfalls sich beschleunigt oder verlangsamt (siehe Reaktorgift). Insofern ist obige Formel der Gesamtnachzerfallswärme sicher nicht sehr präzise. Genauere Nachzerfallsleistungen tragen der exponentiellen Abhängigkeit des radioaktiven Zerfalls Rechnung, enthalten also eine Summe von Expontentialfunktionen, gestalten sich aber insofern schwieriger, als dass sämtliche relevanten Zerfallsketten berücksichtigt werden müssen.

Beispiele für Nachzerfallswärme nach langer Betriebsdauer

Nach 11 Monaten Betrieb, einem typischen Brennelementzyklus, nahe der Nennleistung ergeben sich aus der obigen Formel folgende Werte (Leistungswerte und Zeitdauern sind auf den Brennstoffinhalt eines typischen Großreaktors bezogen):

Zeit nach Abschaltung	Nachzerfallswärme in Prozent	Thermische Leistung in MW bei 4000 MW vor Abschaltung	Zeit für die Erwärmung von 2500 m³ Wasser von 15 °C auf 100 °C^{[Anm. 2]}
10 Sekunden	3,72 %	149	100 min
1 Minute	2,54 %	102	146 min
1 Stunde	1,01 %	40	6 h
1 Tag	0,44 %	18	14 h
3 Tage	0,31 %	13	20 h
1 Woche	0,23 %	9	26 h
1 Monat	0,13 %	5	49 h
3 Monate	0,07 %	3	89 h

Abklingvorgang nach Brennelementwechsel

Auch mehrere Monate nach dem Betrieb können Brennelemente ohne Kühlung wieder den Schmelzpunkt erreichen. Um die Nachzerfallswärme verbrauchter („abgebrannter“) Brennelemente abzuführen, müssen die Brennstäbe noch mehrere Jahre in den zu einem Kraftwerk gehörenden, mit Wasser gefüllten Abklingbecken gelagert werden, die die Wärme wiederum über Kühlkreisläufe abführen.

Siehe auch

Einzelnachweise

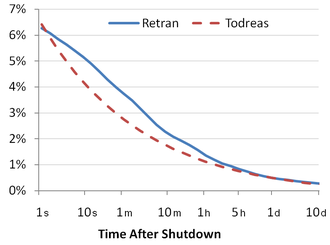
↑ RETRAN-02. Nuclear Power Industry Engineering & Consulting. CSA, abgerufen am 27. März 2011 (englisch).
↑ Neil E. Todreas and Mujid S. Kazimi: Nuclear Systems I, Thermal Hydraulic Fundamentals. 2 Auflage. Hemisphere Publishing Corporation, New York 1990, ISBN 0-89116-935-0.
↑ K. Way, E. P. Wigner: "Radiation from Fission Products", Technical Information Division, United States Atomic Energy Commission, Oak Ridge, Tennessee, 1946. K. Way, E. P. Wigner: "The Rate of Decay of Fission Products", in: Physical Review 73 (1948), 1318–1330.

Anmerkungen

↑ Der Wirkungsgrad des Reaktors entspräche dementsprechend rund 30 %, siehe auch Wirkungsgrad Beispiele
↑ Inhalt eines olympischen Schwimmbeckens

[RETRAN-1] RETRAN-02. Nuclear Power Industry Engineering & Consulting. CSA, abgerufen am 27. März 2011 (englisch).

[TODREAS-2] Neil E. Todreas and Mujid S. Kazimi: Nuclear Systems I, Thermal Hydraulic Fundamentals. 2 Auflage. Hemisphere Publishing Corporation, New York 1990, ISBN 0-89116-935-0.

[4] K. Way, E. P. Wigner: "Radiation from Fission Products", Technical Information Division, United States Atomic Energy Commission, Oak Ridge, Tennessee, 1946. K. Way, E. P. Wigner: "The Rate of Decay of Fission Products", in: Physical Review 73 (1948), 1318–1330.

[3] Der Wirkungsgrad des Reaktors entspräche dementsprechend rund 30 %, siehe auch Wirkungsgrad Beispiele

[5] Inhalt eines olympischen Schwimmbeckens

[1]

[2]

[Anm. 1]

[3]

[Anm. 2]