Interferenz beschreibt die Überlagerung von zwei oder mehr Wellen nach dem Superpositionsprinzip – also die Addition ihrer Amplituden (nicht der Intensitäten) während ihrer Durchdringung. Interferenz tritt bei allen Arten von Wellen auf, also bei Schall-, Licht-, Materiewellen usw.
Löschen sich die Wellen dabei gegenseitig aus, so spricht man von (vollständiger) destruktiver Interferenz. Verstärken sich die Amplituden, so spricht man von konstruktiver Interferenz. Das Muster aus Stellen konstruktiver und destruktiver Interferenz wird als Interferenzmuster bezeichnet. Im experimentellen Aufbau treten abwechselnd charakteristische Interferenzmaxima und Interferenzminima auf. Ein bekanntes Beispiel ist etwa das Streifenmuster hinter einer Doppelspalt-Anordnung. Das Auftreten von Interferenz im physikalischen Experiment gilt als Nachweis für die Wellennatur der untersuchten Strahlung. Dass bei einem Doppelspaltversuch auch dann ein Interferenzmuster beobachtet werden kann, wenn man das Licht (Photonen) durch Elektronen ersetzt, verursachte zu Beginn des 20. Jahrhunderts ein neues Verständnis von Materie. Die destruktive Interferenz ist bei Gravitationswellen physikalisch unmöglich.
Das Wort „Interferenz“ ist ebenso wie das englische interference vom altfranzösischen s’entreferir ‚sich gegenseitig schlagen‘ abgeleitet.[1] Dieses altfranzösische Wort wiederum ist aus der lateinischen Vorsilbe inter (zwischen) und dem Verb ferire ‚schlagen‘ zusammengesetzt.
Auf Interferenz beruhende physikalische Effekte
Schwebung und stehende Welle
Überlagert man zwei Wellen mit ungleichen, aber nahe beieinander liegenden Frequenzen $ \!\ \nu _{1} $ und $ \nu _{2}\,, $ so ergibt sich durch die Schwebung ein Muster, wie es in der ersten Abbildung rechts (unterer Graph) gezeigt ist. Es bildet sich eine schnelle Oszillation aus ($ \nu _{\mathrm {schnell} }={\tfrac {\nu _{1}+\nu _{2}}{2}}\,, $ in dunkelroter Farbe), deren Amplitude sich mit einer langsamen Frequenz ($ \nu _{\mathrm {Schwebung} }={\tfrac {|\nu _{2}-\nu _{1}|}{2}}\,, $blau) ändert.
Zum Stimmen von Musikinstrumenten kann man die entsprechende Einstellung solange verändern, bis man zusammen mit einem Referenzton (bspw. aus einer Stimmgabel) keine Schwebung mehr wahrnimmt. Die Vermessung von Schwebungssignalen kann auch zur Messung von ansonsten (für das Messgerät) zu hohen Frequenzen genutzt werden. Dazu ist allerdings eine Signalquelle notwendig, die Signale mit sehr stabiler und präziser Frequenz liefert.
Die Interferenz zweier Wellen gleicher Wellenlänge, aber mit entgegengesetzter Ausbreitungsrichtung führt zu einer stehenden Welle.
Kohärenz
Das Wellenfeld, das aus der Interferenz zweier (oder mehrerer) Wellen entsteht, kann nur dann zeitlich stabil sein, wenn diese Wellen untereinander eine (zeitlich) feste Phasenbeziehung aufweisen. Man spricht dann von kohärenten Wellen. Sind die Wellen nicht monochromatisch, bestehen also aus einer ganzen Reihe von Frequenzanteilen, so definiert man eine Kohärenzzeit, die beschreibt, wie die Wellen maximal gegeneinander verschoben sein dürfen, um noch ein stabiles Interferenzbild zu erzeugen. Diese Kohärenzzeit (oder die daraus abgeleitete Kohärenzlänge) ist ein wichtiges Maß für physikalische Lichtquellen.
Doppelspaltversuch
Ein bekanntes Experiment, das die Wirkung der Interferenz verdeutlicht, ist der Doppelspaltversuch (Thomas Young, 1802). Dabei wird in einen Elektronen- oder Lichtstrahl eine Blende aus zwei schmalen (Größenordnung einer Wellenlänge) Spalten aufgestellt. Dahinter befindet sich ein Detektor bzw. ein Schirm, auf dem die Elektronen oder Photonen nachgewiesen werden. Ist nur ein Spalt offen, bildet sich das typische Beugungsmuster eines Einfachspaltes. Gibt man beide Spalte frei, so entstehen nicht nur zwei Lichtstreifen, sondern mehrere. Die Streifenabstände verhalten sich umgekehrt proportional zum Abstand der Spalte. Interferenz und Beugung führen dazu, dass sich die Wellen des Lichts wie oben beschrieben überlagern und somit eine Anordnung von hellen und dunklen Streifen bilden. Auf das Doppelspaltexperiment wird weiter unten nochmals im Abschnitt über Interferenz in der Quantenmechanik eingegangen.
Interferometer
In der Messtechnik werden Interferometer eingesetzt. Diese nutzen Interferenzerscheinungen zur Messung von Längen oder Phasenverschiebungen mit sehr hoher Auflösung. Dazu wird ein (Licht-)Strahl in zwei kohärente Teile aufgespaltet, die später wieder überlagert werden. Die beiden Strahlen legen dabei unterschiedliche Strecken $ \!\ s_{1} $ und $ \!\ s_{2} $ zurück. Unterscheiden diese sich um ein ganzzahliges Vielfaches der Wellenlänge, so erhält man am Ausgang des Interferometers konstruktive Interferenz. Unterscheiden sie sich um eine halbe Wellenlänge (Phasenverschiebung $ \Delta \varphi =180^{\circ } $), so erhält man destruktive Interferenz. Stellt man nun das Interferometer zunächst auf konstruktive Interferenz ein und führt dann eine zusätzliche Phasenverschiebung $ \!\ \Delta \varphi $ in einem der beiden Arme ein, so kann man diese über die Intensität am Ausgang des Interferometers bestimmen.
Es gibt verschiedene Umsetzungen dieses Prinzips: Mach-Zehnder-Interferometer, Michelson-Interferometer, Sagnac-Interferometer, Fabry-Pérot-Interferometer etc.
Beugung und Auflösungsvermögen optischer Geräte
Bei der Beugung von Wellen an einem Spalt trifft eine Wellenfront auf einen Spalt. Nach dem Huygensschen Prinzip gehen nun von allen Punkten entlang dem Spalt neue Halbkugelwellen aus, die dahinter interferieren. Dadurch bildet sich das typische Beugungsmuster eines Einfachspaltes (siehe: Abbildung rechts!). Dabei ist das Beugungsmuster umso schmaler, je breiter der Spalt und je kleiner die Wellenlänge ist.
Jedes optische Gerät beinhaltet eine Eintrittsöffnung (z. B.: Öffnung bzw. erste Linse eines Objektives oder Hauptspiegel eines Teleskopes). Diese kann als Spalt modelliert werden und ihr Beugungsbild begrenzt die Auflösung des Gerätes. Diese Begrenzung beruht darauf, dass jedes optische Gerät in irgendeiner Weise ein Bild dieses Eintrittsspaltes erzeugt, das durch die Breite des Beugungsmusters gegeben ist.
Interferenzfarben
Weißes Licht, welches an dünnen Schichten optisch transparenter Materialien reflektiert wird, erscheint häufig farbig. Diese Interferenzfarben entstehen durch Überlagerung der Strahlen, die an der Oberfläche der Schicht und an der unteren Grenzfläche reflektiert werden.
Im Bild unten ist das Prinzip an dünnen Schichten dargestellt. Strahl 2 wird an der Oberfläche zurückgeworfen, Strahl 1 erst nach Passieren der blau dargestellten dünnen Schicht. Er legt einen um die Strecke $ X\Delta =X0Y $ längeren Weg zurück. Ist $ \!\ \Delta $ – auch Gangunterschied genannt – ein ganzes Vielfaches der Wellenlänge $ \lambda \,, $ d. h.:
- $ \Delta =n\lambda \quad {\text{für}}\quad n=0,1,2,\dots \, $
löschen sich die Strahlen 1 und 2 aus. Es gelten genau die Gesetzmäßigkeiten wie für Interferenz am Doppelspalt, nur gerade andersherum, da bei der Reflexion von Strahl 1 am allgemein optisch dichteren Medium eine Phasenverschiebung einer halben Wellenlänge im reflektierten Strahl auftritt. Strahl 2 wird an der unteren Grenzfläche am optisch dünneren Medium reflektiert, so dass hier kein Phasensprung auftritt. Im Bildbeispiel ist es blaues Licht, das destruktiv interferiert. Das Licht anderer Wellenlängen bleibt erhalten. Strahlt man weißes Licht ein, wird es ohne Blauanteil reflektiert. Man sieht gelbes Licht, die Komplementärfarbe zu Blau.
Schemazeichnung zur Entstehung von Interferenzfarben
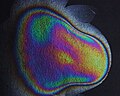
Interferenzfarben im Gefieder der Purpurkehlnymphe
Typisch gut ausgeprägte Interferenzfarben in einer dünnen Oxidschicht auf dem Metall Wismut
Interferenzfarben in gebrochenem Eis
Interferenzfarben in Nagellackschicht
.png)
Ein bekanntes Beispiel für das Auftreten von Interferenzfarben an zwei eng benachbarten Oberflächen sind die newtonschen Ringe.
Ein verwandter Effekt sind Farben, die durch Reflexion von weißem Licht an fein strukturierten Oberflächen entstehen. Die Interferenzfarben entstehen hier aus der Abhängigkeit der Beugung von der Wellenlänge des Lichtes. Die Farben vieler Schmetterlinge und die einiger besonders prächtig schillernder Vögel beruhen auf diesem Effekt.
Weißlichtinterferenz
Die Überlagerung kontinuierlich variierender Wellenlänge und Amplitude (Spektrum) erzeugt ein Interferenzmuster nur innerhalb der Kohärenzlänge. In der Weißlichtinterferometrie wird dieses Verhalten ausgenutzt, um eine eindeutige Längenmessung zu erhalten. Ein weiteres Anwendungsbeispiel findet sich in der Optischen Kohärenztomografie, die dadurch dreidimensionale Strukturen erfassen kann.
Laser-Speckle
Laser sind Lichtquellen mit sehr hoher Kohärenz (großer Kohärenzlänge, typischerweise einige Meter, bis zu wenigen hundert Metern). Dieses führt dazu, dass Laserlicht auch nach der Reflexion an diffusen Oberflächen noch interferenzfähig ist. Dieses erklärt das stabile Punktemuster, das man bei der Reflexion eines Laserstrahles bspw. an einem Blatt Papier beobachtet. Man kann sich das anschaulich so vorstellen: Raumrichtungen, in die wegen konstruktiver Interferenz viel Energie abgestrahlt wird, wechseln sich ab mit unmittelbar benachbarten Raumrichtungen, in welche wenig Energie gelangt. Die sehr kurze Wellenlänge von Licht bewirkt, dass sich diese Raumrichtungen um Bruchteile eines Winkelgrades unterscheiden. Es entsteht ein Strahlungsdiagramm mit sehr vielen Nebenzipfeln, das aussieht wie die Stacheln eines Igels.
Die Voraussetzung für das Auftreten von Speckle-Mustern ist, dass die Oberfläche Rauheiten in der Größenordnung der Wellenlänge des Laser-Lichts aufweist (bei sichtbarem Licht: einige 100 nm).
Antischall
In der Akustik wird Interferenz zur Reduktion von störenden Geräuschen ausgenutzt, siehe Antischall. Dieses Prinzip kommt z. B. in Kopfhörern für Flugzeugpiloten zum Einsatz, um den Maschinenlärm lokal zu dämpfen.[2]
Anwendungen in der Funktechnik
Durch Phasenverschiebung zwischen den Antennenelementen einer Phased-Array-Antenne kann die Beobachtungsrichtung sehr schnell umgeschaltet werden.
Durch genaue Analyse der Phasenverschiebungen zwischen den Einzelantennen von Radioteleskopen kann die Richtung entfernter Strahlungsquellen außerordentlich exakt ermittelt werden.
Ein Antennendiagramm zeigt die Strahlungscharakteristik von Einzelantennen oder Antennengruppen, deren Gestalt durch Interferenz festgelegt wird. Bei der Yagi-Uda-Antenne wird auf diese Weise die Strahlungsenergie in eine schmale Vorwärtskeule gebündelt, wodurch sich die gewünschte Richtwirkung ergibt.
Im Balanced Duplexer wird bei hoher Sendeleistung eine Gasentladungsröhre gezündet, die auf die Wellen fast wie ein Kurzschluss wirkt. Durch geschickte Energieverteilung auf zwei getrennte Zweige eines Hohlleiters mit unterschiedlicher Phasenverschiebung und anschließendes Zusammenführen beider Anteile wird erreicht, dass die Sendeenergie zur Antenne fließt (konstruktive Interferenz) und nicht zum Empfänger (destruktive Interferenz).
Ein Diplexer ermöglicht durch destruktive bzw. konstruktive Interferenz in getrennten Zweigen einer Anordnung aus Hohlleitern, dass zwei Funkgeräte unterschiedlicher Wellenlänge mit einer Antenne betrieben werden können. Auf ähnliche Weise wird in einem Ringkoppler die Summe bzw. Differenz zweier gleichfrequenter Signale gebildet.
Mathematische Darstellung
Eine Welle wird üblicherweise durch eine Funktion von Ort $ \!\ x $ und Zeit $ \!\ t $ geschrieben $ f(\mathbf {x} ,t)\,. $ Dieses bringt zum Ausdruck, dass sich eine Welle sowohl im Raum, als auch in der Zeit ausbreitet. Überlagern sich nun mehrere Wellen $ f_{i}(\mathbf {x} ,t) $ an einem Ort $ \mathbf {x_{0}} \,, $ so lässt sich das Wellenfeld dort als Superposition (Summe) der einzelnen Wellen darstellen:
- $ f_{\mathrm {ges} }(\mathbf {x_{0}} ,t)=\sum \limits _{i}f_{i}(\mathbf {x_{0}} ,t)\, $.
Interferenz zweier Wellen gleicher Frequenz und Amplitude, aber unterschiedlicher Phase
Die Überlagerung zweier Wellen gleicher Frequenz und Amplitude lässt sich anhand der trigonometrischen Additionstheoreme berechnen. Werden die beiden Wellen $ f_{1}(t) $ und $ f_{2}(t) $ mit der gemeinsamen Frequenz $ \omega $, der Amplitude $ a $ und den Phasen $ \varphi _{1} $ und $ \varphi _{2} $ durch
- $ f_{1}(t)=a\cdot \sin(\omega \cdot t+\varphi _{1}) $ und $ f_{2}(t)=a\cdot \sin(\omega \cdot t+\varphi _{2})\, $
beschrieben, so ergibt sich für die resultierende Überlagerung der Wellen
- $ f_{1}(t)+f_{2}(t)=a\left(\sin(\omega t+\varphi _{1})+\sin(\omega t+\varphi _{2})\right)=2a\cos \left({\frac {\varphi _{1}-\varphi _{2}}{2}}\right)\sin \left(\omega t+{\frac {\varphi _{1}+\varphi _{2}}{2}}\right)\, $,
d. h., es entsteht eine Welle derselben Frequenz, deren Amplitude von der Differenz der Phasen der beiden ursprünglichen Wellen abhängt und deren Phase das Mittel der Phasen der ursprünglichen Wellen ist. Für gleiche Phasen der Wellen ($ \varphi _{1}=\varphi _{2} $) wird der Cosinus Eins. Es ergibt sich eine Amplitude von $ 2a $, d. h., die Amplitude verdoppelt sich gegenüber den Ausgangsamplituden, was konstruktiver Interferenz entspricht. Für eine Phasendifferenz von 180°,($ \varphi _{1}=\varphi _{2}+\pi $) wird der Cosinus Null, d. h., die resultierende Welle verschwindet. Dieses entspricht destruktiver Interferenz.
Interferenz zweier Wellen gleicher Frequenz aber unterschiedlicher Amplitude und Phase
Für gleiche Frequenz der Wellen, aber unterschiedliche Amplituden und Phasen lässt sich die resultierende Welle mittels Zeigerarithmetik berechnen. Die beiden Wellen $ g_{1}(t) $ und $ g_{2}(t) $ besitzen die gemeinsame Frequenz $ \omega $, die Amplituden $ a_{1} $ und $ a_{2} $ und die Phasen $ \varphi _{1} $ und $ \varphi _{2} $
- $ g_{1}(t)=a_{1}\cdot \sin(\omega t+\varphi _{1}) $ und $ g_{2}(t)=a_{2}\cdot \sin(\omega t+\varphi _{2})\, $.
Die resultierende Überlagerung der Wellen hat die Form:
- $ g_{1}(t)+g_{2}(t)=A\cdot \sin(\omega t+\varphi )\, $
mit der Amplitude:
- $ A={\sqrt {a_{1}^{2}+a_{2}^{2}+2a_{1}a_{2}\cos(\varphi _{1}-\varphi _{2})}}\, $
und der Phase $ \varphi $
- $ \tan \varphi ={\frac {a_{1}\sin(\varphi _{1})+a_{2}\sin(\varphi _{2})}{a_{1}\cos(\varphi _{1})+a_{2}\cos(\varphi _{2})}}\, $.
Überlagerung von Kreiswellen
Die Abbildung links zeigt die Interferenz von zwei kreisförmigen Wellengruppen gleicher Wellenlänge und Amplitude. Die Kreuze markieren die Lage der Quellen, die Kreise die Maxima der jeweiligen Teilwelle. An weißen Stellen tritt konstruktive Interferenz, in positiver Richtung, an schwarzen konstruktive Interferenz, in negativer Richtung, auf. An den grauen Stellen herrscht destruktive Interferenz. Es ist zu erkennen, dass die Minima auf einer Hyperbelschar liegen, deren Brennpunkte identisch den Quellorten der Wellen sind. Man spricht deshalb bei zwei Punktquellen von einer hyperbolischen Interferenz. Die Hyperbel ist dabei die Kurve aller Punkte, die zu den zwei Quellorten die Laufzeitdifferenz $ t={\tfrac {\lambda }{2}} $ haben. Der Scheitelpunktabstand $ \!\ 2a $ entspricht der Laufzeitdifferenz $ \!\ 2a=(T_{1}-T_{2})v $, wenn $ \!\ T_{1} $ und $ \!\ T_{2} $ den Zeitbezug der beiden speisenden Zeitfunktionen darstellen und $ v $ die mediale Ausbreitungsgeschwindigkeit darstellt.
In der rechten Abbildung wird die Veränderung des Interferenzbildes in Abhängigkeit von der Wellenlänge (nimmt von oben nach unten zu) und in Abhängigkeit vom Abstand der Quellen (nimmt von links nach rechts zu) demonstriert. In den dunklen Bereichen (um die Interferenzminima) liegt destruktive und in den hellen (Maxima) konstruktive Interferenz vor.
Simulierte Interferenz von zwei kreisförmigen Wellengruppen gleicher Wellenlänge und Amplitude.
Interferenz zweier Kreiswellen in Abhängigkeit von der Wellenlänge und dem Quellenabstand.
Interferenz in der Quantenmechanik
Anschauliche Erklärung
In der Quantenmechanik spielen Interferenzphänomene eine entscheidende Rolle. Teilchen (und allgemeiner beliebige Zustände eines Systems) werden durch Wellenfunktionen beschrieben. Diese sind die Lösungen der Schrödingergleichung, die eine Form ähnlich einer Wellengleichung annehmen kann. Damit können sich Teilchen, also Materie, in der Quantenmechanik wie Wellen verhalten und auch interferieren (siehe auch Welle-Teilchen-Dualismus, Materiewellen). Ein bekanntes Beispiel ist etwa die Interferenz von Elektronen in einem Doppelspaltexperiment[3] (siehe auch: die Bilder rechts!) oder die Interferenz zweier Bose-Einstein-Kondensate.
Der Arbeitsgruppe von Anton Zeilinger ist es 1999 gelungen, ein Interferenzmuster von Fullerenen (Molekülen aus 60 oder 70 Kohlenstoff-Atomen) zu beobachten. Dieses sind bei weitem nicht die schwersten Teilchen, für die Quanteninterferenz beobachtet werden konnte.[4][5] Die Forschungsgruppe rund um Markus Arndt setzte die von Zeilinger initiierten Experimente an der Universität Wien fort und konnte 2010 Quanteninterferenz mit Molekülen aus bis zu 430 Atomen und Massen bis fast 7000 Atomaren Masseneinheiten zeigen.[6]
Bemerkenswert an dieser Form von Interferenz ist allerdings, dass die Messung, welchen Weg ein Quantenobjekt gewählt hat („Welcher-Weg“-Information), dazu führt, dass auch nur noch dieser „benutzt“ wird – also keine Interferenz auftritt. In einer Doppelspaltanordnung hängt das Interferenzmuster also davon ab, ob man herausfinden kann, welchen Weg (durch Spalt 1 oder Spalt 2) das Quantenobjekt nahm. Dies gilt auch, wenn der Weg des Quantenobjekts nicht schon beim Passieren der Spalte sondern erst später festgestellt wird (verzögerter Messprozess). Nur wenn eine Gewinnung der „Welcher-Weg“-Information nie erfolgte oder sie durch einen Quantenradierer wieder getilgt wurde, ergibt sich hinter dem Doppelspalt ein Interferenzbild.[7]
Mathematische Fassung
In der Bra-Ket-Notation lässt sich ein beliebiger quantenmechanischer Zustand in einer orthonormierten Basis $ \{|i\rangle \} $ ($ \langle i|j\rangle =\delta _{ij} $) darstellen. Dabei sind die $ c_{i},b_{i}\in \mathbb {C} $ komplexe Koeffizienten:
- $ |\psi \rangle =\sum \limits _{i}c_{i}\cdot |i\rangle ,\ \ \ \ \ \ \ \ \ \ |\phi \rangle =\sum \limits _{i}b_{i}\cdot |i\rangle \, $
Für die Wahrscheinlichkeit, dass ein System im Zustand $ |\psi \rangle $ im Zustand $ |\phi \rangle $ gemessen wird lautet dann:
- $ {\mathcal {P}}(\psi \rightarrow \phi )=|\langle \psi |\phi \rangle |^{2}=\left|\sum \limits _{i}c_{i}^{\ast }b_{i}\right|^{2}=\sum \limits _{i,j}c_{i}^{\ast }c_{j}b_{i}^{\ast }b_{j}=\sum \limits _{i}|c_{i}|^{2}|b_{i}|^{2}+\sum \limits _{i\neq j}c_{i}^{\ast }c_{j}b_{i}^{\ast }b_{j}\, $
Wichtig ist hier, dass nicht die Aufenthaltswahrscheinlichkeiten der Teilchen $ \rho (x)=|\langle x|\psi \rangle |^{2} $ überlagert werden, sondern die (komplexen) Wellenfunktionen selbst. Würden die Aufenthaltswahrscheinlichkeiten überlagert, so würde man in obiger Formel den hinteren Interferenzanteil verlieren und das Interferenzmuster verschwindet.
De Broglie postulierte bereits Anfang des 20. Jahrhunderts, dass allen massiven Teilchen eine Wellenlänge $ \lambda ={\tfrac {h}{p}} $ zugeschrieben werden kann, wobei $ \!\ p $ der Impuls des Teilchens ist und $ \!\ h $ das Plancksche Wirkungsquantum. Mit dieser Wellenlänge kann man direkt die Wellenfunktion $ f({\vec {x}},t) $ für ein Teilchen konstruieren und so die Interferenzmuster mit den weiter oben für Licht beschriebenen Methoden berechnen.
Siehe auch
- Monsterwellen als Beispiel für komplexere, nichtlineare Interferenzen
- Stehende Welle
Literatur
- Claude Cohen-Tannoudji, Bernard Diu, Franck Laloë, Joachim Streubel, Jochen Balla: Quantenmechanik. Band 1. 3. Auflage. Walter de Gruyter, Berlin, New York 2007, ISBN 3-110-19324-8.
- Claude Cohen-Tannoudji, Bernard Diu, Franck Laloe: Quantenmechanik. Band 2. 3. Auflage. Walter de Gruyter, Berlin, New York 2008, ISBN 3-110-20149-6.
Weblinks
Commons: Interferenz – Sammlung von Bildern, Videos und Audiodateien
- Interaktive Animationen zur Interferenz und Überlagerung von Wellen
- Graphische Lösung von Überlagerungen
- Simulationen mit Zeitfunktionen
- Online-Rechner für Interferenzfarben an dünnen Schichten
- Vorlesung Physik III, 59. Stunde, beinhaltet das Thema Interferenz und Kohärenz (Uni Tübingen)
- Bedeutung der Interferenz in der Audiotechnik (incl. Grafiken)
- Interferenz von einzelnen Photonen im Interferometer mit Quantenradierer (QuantumLab)
- Acht Grundversuche zur Interferenz in der Übersicht (LEIFI-Physik)
- Simulation zu Interferenz zweier stehender Wellen
- Animierter Film zur Farbe von Seifenblasen (englisch)
Einzelnachweise
- ↑ Concise Oxford Dictionary, ISBN 0-19-861200-1
- ↑ Katja Bammel: Schall gegen Schall – aktive Lärmunterdrückung. Physik Journal Februar 2007, S. 42–43
- ↑ A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki and H. Ezawa: Demonstration of single-electron build-up of an interference pattern. American Journal of Physics 57 (1989), 117–120
- ↑ Markus Arndt, Olaf Nairz, Julian Voss-Andreae, Claudia Keller, Gerbrand van der Zouw und Anton Zeilinger: Wave–particle duality of C60 molecules, Nature 401 (1999), 680–682, PDF
- ↑ Björn Brezger, Lucia Hackermüller, Stefan Uttenthaler, Julia Petschinka, Markus Arndt und Anton Zeilinger: Matter-Wave Interferometer for Large Molecules, Physical Review Letters 88 (2002), 100404, (Online)
- ↑ "Quantum interference of large organic molecules", Stefan Gerlich, Sandra Eibenberger, Mathias Tomandl, Stefan Nimmrichter, Klaus Hornberger, Paul J. Fagan, Jens Tüxen, Marcel Mayor & Markus Arndt, Nature Communications 2, Article 263; doi:10.1038/ncomms1263, http://www.nature.com/ncomms/journal/v2/n4/full/ncomms1263.html
- ↑ Michael Springer: Welle oder Teilchen – ein Test mit dem Quantenradierer. In: Spektrum der Wissenschaft. 1, Spektrum der Wissenschaft Akademischer Verlag, 1996.
