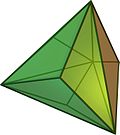
Catalanischer Körper
Ein catalanischer Körper oder auch dual-archimedischer Körper ist ein Körper, der sich zu einem archimedischen Körper dual verhält. So ist zum Beispiel das Rhombendodekaeder dual zum Kuboktaeder. Benannt sind die catalanischen Körper – von denen es dreizehn gibt – nach dem belgischen Mathematiker Eugène Charles Catalan.
Die dual-archimedischen Körper bestehen nur aus einer Flächenart, nämlich identischen nichtregelmäßigen Vielecken, haben aber mindestens zwei verschiedene Arten von Ecken (das Rhombendodekaeder hat zum Beispiel Ecken, an die drei Rhomben, und solche, an die vier Rhomben grenzen). Damit sind sie keine archimedischen Körper im ursprünglichen Sinne mehr.
Allen catalanischen Körpern ist gemein, dass sie eine Inkugel, die sämtliche Flächen von innen berührt, aufweisen. Außerdem existiert eine Kantenkugel, die sämtliche Kanten von innen berührt. Alle Diederwinkel eines catalanischen Körpers sind gleich.
| Catalanischer Körper | Bild | Dualer Körper | Flächen | Ecken | Kanten | Flächenform | Symmetrie |
|---|---|---|---|---|---|---|---|
| Triakistetraeder |  (Animation) |
Tetraederstumpf | 12 | 8 | 18 | gleichschenkliges Dreieck | $ T_{d}\ $ |
| Rhombendodekaeder |  (Animation) |
Kuboktaeder | 12 | 14 | 24 | Rhombus | $ O_{h}\ $ |
| Tetrakishexaeder |  (Animation) |
Oktaederstumpf | 24 | 14 | 36 | gleichschenkliges Dreieck | $ O_{h}\ $ |
| Triakisoktaeder |  (Animation) |
Hexaederstumpf | 24 | 14 | 36 | gleichschenkliges Dreieck | $ O_{h}\ $ |
| Deltoidalikositetraeder |  (Animation) |
Rhombenkuboktaeder | 24 | 26 | 48 | Deltoid | $ O_{h}\ $ |
| Pentagonikositetraeder (zwei spiegelbildlich entgegengesetzte Varianten) |
 (Animation)  (Animation) |
abgeschrägtes Hexaeder | 24 | 38 | 60 | unregelmäßiges Fünfeck | $ O\ $ |
| Rhombentriakontaeder |  (Animation) |
Ikosidodekaeder | 30 | 32 | 60 | Rhombus | $ I_{h}\ $ |
| Hexakisoktaeder oder Disdyakisdodekaeder |
 (Animation) |
Kuboktaederstumpf | 48 | 26 | 72 | unregelmäßiges Dreieck | $ O_{h}\ $ |
| Pentakisdodekaeder |  (Animation) |
Ikosaederstumpf | 60 | 32 | 90 | gleichschenkliges Dreieck | $ I_{h}\ $ |
| Triakisikosaeder |  (Animation) |
Dodekaederstumpf | 60 | 32 | 90 | gleichschenkliges Dreieck | $ I_{h}\ $ |
| Deltoidalhexakontaeder |  (Animation) |
Rhombenikosidodekaeder | 60 | 62 | 120 | Deltoid | $ I_{h}\ $ |
| Pentagonhexakontaeder (zwei spiegelbildlich entgegengesetzte Varianten) |
 (Animation)  (Animation) |
abgeschrägtes Dodekaeder | 60 | 92 | 150 | unregelmäßiges Fünfeck | $ I\ $ |
| Hexakisikosaeder oder Disdyakistriakontaeder |
 (Animation) |
Ikosidodekaederstumpf | 120 | 62 | 180 | unregelmäßiges Dreieck | $ I_{h}\ $ |
Siehe auch
Weblinks
Commons: Catalanische Körper – Sammlung von Bildern, Videos und Audiodateien
Triakistetraeder · Rhombendodekaeder · Tetrakishexaeder · Triakisoktaeder · Deltoidalikositetraeder · Pentagonikositetraeder · Rhombentriakontaeder · Hexakisoktaeder · Pentakisdodekaeder · Triakisikosaeder · Deltoidalhexakontaeder · Pentagonhexakontaeder · Hexakisikosaeder