Johnson-Körper
Die Johnson-Körper sind eine Klasse geometrischer Körper.
Eigenschaften
Johnson-Körper sind streng konvexe Polyeder, die ausschließlich aus regelmäßigen Vielecken aufgebaut sind, aber weder platonische Körper, archimedische Körper, Prismen noch Antiprismen sind. Gemeinsam mit den catalanischen Körpern ist, dass die Ecken eines Johnson-Körpers nicht identisch sind. Eine Besonderheit unter den Johnson-Körpern ist das Pseudo-Rhombenkuboktaeder (J37), dessen Ecken zwar lokal uniform sind, aber nicht global.
1966 veröffentlichte Norman Johnson eine Liste von 92 derartigen Polyedern, von der er annahm, dass sie vollständig ist.[1] Diese Annahme wurde 1969 von Wictor Salgaller bewiesen.[2]
Liste
Auf einen Johnson-Körper wird sich oft mit Jn bezogen, wobei n die Nummer des Körpers in der folgenden Liste ist. Beispielsweise ist die Dreieckskuppel J3.
In der folgenden Liste ist E die Anzahl der Ecken, K die Anzahl der Kanten, Fn die Anzahl der n-eckigen Flächen und F:=F3+F4+F5+... die Anzahl aller Flächen des jeweiligen Körpers.
Pyramiden, Kuppeln und Rotunden
| Jn | Körper | Abbildung | Typ | E | K | F | F3 | F4 | F5 | F6 | F8 | F10 | Symmetrie |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Quadratpyramide | 
|
Pyramide | 5 | 8 | 5 | 4 | 1 | 0 | 0 | 0 | 0 | C4v |
| 2 | Fünfeckpyramide | 
|
Pyramide | 6 | 10 | 6 | 5 | 0 | 1 | 0 | 0 | 0 | C5v |
| 3 | Dreieckskuppel | 
|
Kuppel | 9 | 15 | 8 | 4 | 3 | 0 | 1 | 0 | 0 | C3v |
| 4 | Quadratkuppel | 
|
Kuppel | 12 | 20 | 10 | 4 | 5 | 0 | 0 | 1 | 0 | C4v |
| 5 | Fünfeckskuppel | 
|
Kuppel | 15 | 25 | 12 | 5 | 5 | 1 | 0 | 0 | 1 | C5v |
| 6 | Fünfecksrotunde | 
|
Rotunde | 20 | 35 | 17 | 10 | 0 | 6 | 0 | 0 | 1 | C5v |
modifizierte Pyramiden
| Jn | Name | Abbildung | Typ | E | K | F | F3 | F4 | F5 | Symmetrie |
|---|---|---|---|---|---|---|---|---|---|---|
| 7 | verlängerte Dreieckpyramide | 
|
verlängerte Pyramide | 7 | 12 | 7 | 4 | 3 | 0 | C3v |
| 8 | verlängerte Quadratpyramide (gleichzeitig erweitertes Hexaeder bzw. Quadratprisma) | 
|
verlängerte Pyramide | 9 | 16 | 9 | 4 | 5 | 0 | C4v |
| 9 | verlängerte Fünfeckpyramide |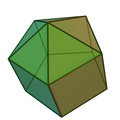 
|
verlängerte Pyramide | 11 | 20 | 11 | 5 | 5 | 1 | C5v |
| 10 | verdreht verlängerte Quadratpyramide | 
|
verdreht verlängerte Pyramide | 9 | 20 | 13 | 12 | 1 | 0 | C4v |
| 11 | verdreht verlängerte Fünfeckpyramide (beschnittenes Ikosaeder) | 
|
verdreht verlängerte Pyramide | 11 | 25 | 16 | 15 | 0 | 1 | C5v |
| 12 | Dreiecksbipyramide | 
|
Bipyramide | 5 | 9 | 6 | 6 | 0 | 0 | D3h |
| 13 | Fünfecksbipyramide | 
|
Bipyramide | 7 | 15 | 10 | 10 | 0 | 0 | D5h |
| 14 | verlängerte Dreiecksbipyramide | 
|
verlängerte Bipyramide | 8 | 15 | 9 | 6 | 3 | 0 | D3h |
| 15 | verlängerte Quadratbipyramide (gleichzeitig zweifach erweitertes Hexaeder bzw. Quadratprisma) | 
|
verlängerte Bipyramide | 10 | 20 | 12 | 8 | 4 | 0 | D4h |
| 16 | verlängerte Fünfecksbipyramide | 
|
verlängerte Bipyramide | 12 | 25 | 15 | 10 | 5 | 0 | D5h |
| 17 | verdreht verlängerte Quadratbipyramide | 
|
verdreht verlängerte Bipyramide | 10 | 24 | 16 | 16 | 0 | 0 | D4d |
modifizierte Kuppeln und Rotunden
| Jn | Körper | Abbildung | Typ | E | K | F | F3 | F4 | F5 | F6 | F8 | F10 | Symmetrie |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 18 | verlängerte Dreieckskuppel | 
|
verlängerte Kuppel | 15 | 27 | 14 | 4 | 9 | 0 | 1 | 0 | 0 | C3v |
| 19 | verlängerte Quadratkuppel (Beschnittenes kleines Rhombenkuboktaeder) |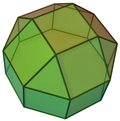 
|
verlängerte Kuppel | 20 | 36 | 18 | 4 | 13 | 0 | 0 | 1 | 0 | C4v |
| 20 | verlängerte Fünfeckskuppel | 
|
verlängerte Kuppel | 25 | 45 | 22 | 5 | 15 | 1 | 0 | 0 | 1 | C5v |
| 21 | verlängerte Fünfecksrotunde | 
|
verlängerte Rotunde | 30 | 55 | 27 | 10 | 10 | 6 | 0 | 0 | 1 | C5v |
| 22 | verdreht verlängerte Dreieckskuppel | 
|
verdreht verlängerte Kuppel | 15 | 33 | 20 | 16 | 3 | 0 | 1 | 0 | 0 | C3v |
| 23 | verdreht verlängerte Quadratkuppel | 
|
verdreht verlängerte Kuppel | 20 | 44 | 26 | 20 | 5 | 0 | 0 | 1 | 0 | C4v |
| 24 | verdreht verlängerte Fünfeckskuppel | 
|
verdreht verlängerte Kuppel | 25 | 55 | 32 | 25 | 5 | 1 | 0 | 0 | 1 | C5v |
| 25 | verdreht verlängerte Fünfecksrotunde | 
|
verdreht verlängerte Rotunde | 30 | 65 | 37 | 30 | 0 | 6 | 0 | 0 | 1 | C5v |
| 26 | verdrehter Doppelkeil | 
|
Doppelkuppel | 8 | 14 | 8 | 4 | 4 | 0 | 0 | 0 | 0 | D2d |
| 27 | Dreiecksdoppelkuppel (verdrehtes Kuboktaeder, Disheptaeder) | 
|
Doppelkuppel | 12 | 24 | 14 | 8 | 6 | 0 | 0 | 0 | 0 | D3h |
| 28 | Quadratdoppelkuppel | 
|
Doppelkuppel | 16 | 32 | 18 | 8 | 10 | 0 | 0 | 0 | 0 | D4h |
| 29 | verdrehte Quadratdoppelkuppel | 
|
Doppelkuppel | 16 | 32 | 18 | 8 | 10 | 0 | 0 | 0 | 0 | D4d |
| 30 | Fünfecksdoppelkuppel | 
|
Doppelkuppel | 20 | 40 | 22 | 10 | 10 | 2 | 0 | 0 | 0 | D5h |
| 31 | verdrehte Fünfecksdoppelkuppel | 
|
Doppelkuppel | 20 | 40 | 22 | 10 | 10 | 2 | 0 | 0 | 0 | D5d |
| 32 | Fünfeckskuppelrotunde | 
|
Kuppelrotunde | 25 | 50 | 27 | 15 | 5 | 7 | 0 | 0 | 0 | C5v |
| 33 | verdrehte Fünfeckskuppelrotunde | 
|
Kuppelrotunde | 25 | 50 | 27 | 15 | 5 | 7 | 0 | 0 | 0 | C5v |
| 34 | Fünfecksdoppelrotunde (verdrehtes Ikosidodekaeder) | 
|
Doppelrotunde | 30 | 60 | 32 | 20 | 0 | 12 | 0 | 0 | 0 | D5h |
| 35 | verlängerte Dreiecksdoppelkuppel | 
|
verlängerte Doppelkuppel | 18 | 36 | 20 | 8 | 12 | 0 | 0 | 0 | 0 | D3h |
| 36 | verlängerte verdrehte Dreiecksdoppelkuppel | 
|
verlängerte Doppelkuppel | 18 | 36 | 20 | 8 | 12 | 0 | 0 | 0 | 0 | D3d |
| 37 | verlängerte verdrehte Quadratsdoppelkuppel (verdrehtes kleines Rhombenkuboktaeder) | 
|
verlängerte Doppelkuppel | 24 | 48 | 26 | 8 | 18 | 0 | 0 | 0 | 0 | D4d |
| 38 | verlängerte Fünfecksdoppelkuppel | 
|
verlängerte Doppelkuppel | 30 | 60 | 32 | 10 | 20 | 2 | 0 | 0 | 0 | D5h |
| 39 | verlängerte verdrehte Fünfecksdoppelkuppel | 
|
verlängerte Doppelkuppel | 30 | 60 | 32 | 10 | 20 | 2 | 0 | 0 | 0 | D5d |
| 40 | verlängerte Fünfeckskuppelrotunde | 
|
verlängerte Kuppelrotunde | 35 | 70 | 37 | 15 | 15 | 7 | 0 | 0 | 0 | C5v |
| 41 | verlängerte verdrehte Fünfeckskuppelrotunde | 
|
verlängerte Kuppelrotunde | 35 | 70 | 37 | 15 | 15 | 7 | 0 | 0 | 0 | C5v |
| 42 | verlängerte Fünfecksdoppelrotunde | Datei:Elongated pentagonal orthobirotunda.png | verlängerte Doppelrotunde | 40 | 80 | 42 | 20 | 10 | 12 | 0 | 0 | 0 | D5h |
| 43 | verlängerte verdrehte Fünfecksdoppelrotunde | Datei:Elongated pentagonal gyrobirotunda.png | verlängerte Doppelrotunde | 40 | 80 | 42 | 20 | 10 | 12 | 0 | 0 | 0 | D5d |
| 44 | verdreht verlängerte Dreiecksdoppelkuppel | Datei:Gyroelongated triangular bicupola.png | verdreht verlängerte Doppelkuppel | 18 | 42 | 26 | 20 | 6 | 0 | 0 | 0 | 0 | D3 |
| 45 | verdreht verlängerte Quadratdoppelkuppel | Datei:Gyroelongated square bicupola.png | verdreht verlängerte Doppelkuppel | 24 | 56 | 34 | 24 | 10 | 0 | 0 | 0 | 0 | D4 |
| 46 | verdreht verlängerte Fünfecksdoppelkuppel | Datei:Gyroelongated pentagonal bicupola.png | verdreht verlängerte Doppelkuppel | 30 | 70 | 42 | 30 | 10 | 2 | 0 | 0 | 0 | D5 |
| 47 | verdreht verlängerte Fünfeckskuppelrotunde | Datei:Gyroelongated pentagonal cupolarotunda.png | verdreht verlängerte Kuppelrotunde | 35 | 80 | 47 | 35 | 5 | 7 | 0 | 0 | 0 | C5 |
| 48 | verdreht verlängerte Fünfecksdoppelrotunde | Datei:Gyroelongated pentagonal birotunda.png | verdreht verlängerte Doppelrotunde | 40 | 90 | 52 | 40 | 0 | 12 | 0 | 0 | 0 | D5 |
erweiterte Prismen
| Jn | Körper | Abbildung | E | K | F | F3 | F4 | F5 | F6 | Symmetrie |
|---|---|---|---|---|---|---|---|---|---|---|
| 49 | erweitertes Dreiecksprisma | Datei:Augmented triangular prism.png | 7 | 13 | 8 | 6 | 2 | 0 | 0 | C2v |
| 50 | doppelt erweitertes Dreiecksprisma | Datei:Biaugmented triangular prism.png | 8 | 17 | 11 | 10 | 1 | 0 | 0 | C2v |
| 51 | dreifach erweitertes Dreiecksprisma | Datei:Triaugmented triangular prism.png | 9 | 21 | 14 | 14 | 0 | 0 | 0 | D3h |
| 52 | erweitertes Fünfecksprisma | Datei:Augmented pentagonal prism.png | 11 | 19 | 10 | 4 | 4 | 2 | 0 | C2v |
| 53 | doppelt erweitertes Fünfecksprisma | Datei:Biaugmented pentagonal prism.png | 12 | 23 | 13 | 8 | 3 | 2 | 0 | C2v |
| 54 | erweitertes Sechsecksprisma | Datei:Augmented hexagonal prism.png | 13 | 22 | 11 | 4 | 5 | 0 | 2 | C2v |
| 55 | doppelt erweitertes Sechsecksprisma (para) | Datei:Parabiaugmented hexagonal prism.png | 14 | 26 | 14 | 8 | 4 | 0 | 2 | D2h |
| 56 | doppelt erweitertes Sechsecksprisma (meta) | Datei:Metabiaugmented hexagonal prism.png | 14 | 26 | 14 | 8 | 4 | 0 | 2 | C2v |
| 57 | dreifach erweitertes Sechsecksprisma | Datei:Triaugmented hexagonal prism.png | 15 | 30 | 17 | 12 | 3 | 0 | 2 | D3h |
modifizierte platonische Körper
| Jn | Körper | Abbildung | Typ | E | K | F | F3 | F4 | F5 | Symmetrie |
|---|---|---|---|---|---|---|---|---|---|---|
| 58 | erweitertes Dodekaeder | Datei:Augmented dodecahedron.png | erweitertes Dodekaeder | 21 | 35 | 16 | 5 | 0 | 11 | C5v |
| 59 | doppelt erweitertes Dodekaeder (para) | Datei:Parabiaugmented dodecahedron.png | erweitertes Dodekaeder | 22 | 40 | 20 | 10 | 0 | 10 | D5d |
| 60 | doppelt erweitertes Dodekaeder (meta) | Datei:Metabiaugmented dodecahedron.png | erweitertes Dodekaeder | 22 | 40 | 20 | 10 | 0 | 10 | C2v |
| 61 | dreifach erweitertes Dodekaeder | Datei:Triaugmented dodecahedron.png | erweitertes Dodekaeder | 23 | 45 | 24 | 15 | 0 | 9 | C3v |
| 62 | doppelt beschnittenes Ikosaeder (meta) | Datei:Metabidiminished icosahedron.png | beschnittenes Ikosaeder | 10 | 20 | 12 | 10 | 0 | 2 | C2v |
| 63 | dreifach beschnittenes Ikosaeder | Datei:Tridiminished icosahedron.png | beschnittenes Ikosaeder | 9 | 15 | 8 | 5 | 0 | 3 | C3v |
| 64 | erweitertes dreifach beschnittenes Ikosaeder | Datei:Augmented tridiminished icosahedron.png | - | 10 | 18 | 10 | 7 | 0 | 3 | C3v |
modifizierte archimedische Körper
| Jn | Körper | Abbildung | Typ | E | K | F | F3 | F4 | F5 | F6 | F8 | F10 | Symmetrie |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 65 | erweitertes abgestumpftes Tetraeder | Datei:Augmented truncated tetrahedron.png | erweitertes abgestumpftes Tetraeder | 15 | 27 | 14 | 8 | 3 | 0 | 3 | 0 | 0 | C3v |
| 66 | erweitertes abgestumpftes Hexaeder | Datei:Augmented truncated cube.png | erweitertes abgestumpftes Hexaeder | 28 | 48 | 22 | 12 | 5 | 0 | 0 | 5 | 0 | C4v |
| 67 | doppelt erweitertes abgestumpftes Hexaeder | Datei:Biaugmented truncated cube.png | erweitertes abgestumpftes Hexaeder | 32 | 60 | 30 | 16 | 10 | 0 | 0 | 4 | 0 | D4h |
| 68 | erweitertes abgestumpftes Dodekaeder | Datei:Augmented truncated dodecahedron.png | erweitertes abgestumpftes Dodekaeder | 65 | 105 | 42 | 25 | 5 | 1 | 0 | 0 | 11 | C5v |
| 69 | doppelt erweitertes abgestumpftes Dodekaeder (para) | Datei:Parabiaugmented truncated dodecahedron.png | erweitertes abgestumpftes Dodekaeder | 70 | 120 | 52 | 30 | 10 | 2 | 0 | 0 | 10 | D5d |
| 70 | doppelt erweitertes abgestumpftes Dodekaeder (meta) | Datei:Metabiaugmented truncated dodecahedron.png | erweitertes abgestumpftes Dodekaeder | 70 | 120 | 52 | 30 | 10 | 2 | 0 | 0 | 10 | C2v |
| 71 | dreifach erweitertes abgestumpftes Dodekaeder | Datei:Triaugmented truncated dodecahedron.png | erweitertes abgestumpftes Dodekaeder | 75 | 135 | 62 | 35 | 15 | 3 | 0 | 0 | 9 | C3v |
| 72 | verdrehtes Rhombenikosidodekaeder | Datei:Gyrate rhombicosidodecahedron.png | verdrehtes kleines Rhombenikosidodekaeder | 60 | 120 | 62 | 20 | 30 | 12 | 0 | 0 | 0 | C5v |
| 73 | doppelt verdrehtes kleines Rhombenikosidodekaeder (para) | Datei:Parabigyrate rhombicosidodecahedron.png | verdrehtes kleines Rhombenikosidodekaeder | 60 | 120 | 62 | 20 | 30 | 12 | 0 | 0 | 0 | D5d |
| 74 | doppelt verdrehtes kleines Rhombenikosidodekaeder (meta) | Datei:Metabigyrate rhombicosidodecahedron.png | verdrehtes kleines Rhombenikosidodekaeder | 60 | 120 | 62 | 20 | 30 | 12 | 0 | 0 | 0 | C2v |
| 75 | dreifach verdrehtes kleines Rhombenikosidodekaeder | Datei:Trigyrate rhombicosidodecahedron.png | verdrehtes kleines Rhombenikosidodekaeder | 60 | 120 | 62 | 20 | 30 | 12 | 0 | 0 | 0 | C3v |
| 76 | Beschnittenes kleines Rhombenikosidodekaeder | Datei:Diminished rhombicosidodecahedron.png | beschnittenes kleines Rhombenikosidodekaeder | 55 | 105 | 52 | 15 | 25 | 11 | 0 | 0 | 1 | C5v |
| 77 | verdrehtes beschnittenes kleines Rhombenikosidodekaeder (para) | Datei:Paragyrate diminished rhombicosidodecahedron.png | verdrehtes beschnittenes kleines Rhombenikosidodekaeder | 55 | 105 | 52 | 15 | 25 | 11 | 0 | 0 | 1 | C5v |
| 78 | verdrehtes beschnittenes kleines Rhombenikosidodekaeder (meta) | Datei:Metagyrate diminished rhombicosidodecahedron.png | verdrehtes beschnittenes kleines Rhombenikosidodekaeder | 55 | 105 | 52 | 15 | 25 | 11 | 0 | 0 | 1 | Cs |
| 79 | doppelt verdrehtes beschnittenes kleines Rhombenikosidodekaeder | Datei:Bigyrate diminished rhombicosidodecahedron.png | verdrehtes beschnittenes kleines Rhombenikosidodekaeder | 55 | 105 | 52 | 15 | 25 | 11 | 0 | 0 | 1 | Cs |
| 80 | doppelt beschnittenes kleines Rhombenikosidodekaeder (para) | Datei:Parabidiminished rhombicosidodecahedron.png | beschnittenes kleines Rhombenikosidodekaeder | 50 | 90 | 42 | 10 | 20 | 10 | 0 | 0 | 2 | D5d |
| 81 | doppelt beschnittenes kleines Rhombenikosidodekaeder (meta) | Datei:Metabidiminished rhombicosidodecahedron.png | beschnittenes kleines Rhombenikosidodekaeder | 50 | 90 | 42 | 10 | 20 | 10 | 0 | 0 | 2 | C2v |
| 82 | verdrehtes doppelt beschnittenes kleines Rhombenikosidodekaeder | Datei:Gyrate bidiminished rhombicosidodecahedron.png | verdrehtes beschnittenes kleines Rhombenikosidodekaeder | 50 | 90 | 42 | 10 | 20 | 10 | 0 | 0 | 2 | C2v |
| 83 | dreifach beschnittenes kleines Rhombenikosidodekaeder | Datei:Tridiminished rhombicosidodecahedron.png | beschnittenes kleines Rhombenikosidodekaeder | 45 | 75 | 32 | 5 | 15 | 9 | 0 | 0 | 3 | C3v |
Übrige
| Jn | Körper | Abbildung | E | K | F | F3 | F4 | F5 | F6 | Symmetrie |
|---|---|---|---|---|---|---|---|---|---|---|
| 84 | Trigondodekaeder | Datei:Snub disphenoid.png | 8 | 18 | 12 | 12 | 0 | 0 | 0 | D2d |
| 85 | Abgeschrägtes Quadratantiprisma | Datei:Snub square antiprism.png | 16 | 40 | 26 | 24 | 2 | 0 | 0 | D4d |
| 86 | Sphenocorona | Datei:Sphenocorona.png | 10 | 22 | 14 | 12 | 2 | 0 | 0 | C2v |
| 87 | Erweiterte Sphenocorona | Datei:Augmented sphenocorona.png | 11 | 26 | 17 | 16 | 1 | 0 | 0 | Cs |
| 88 | Sphenomegacorona | Datei:Sphenomegacorona.png | 12 | 28 | 18 | 16 | 2 | 0 | 0 | C2v |
| 89 | Hebesphenomegacorona | Datei:Hebesphenomegacorona.png | 14 | 33 | 21 | 18 | 3 | 0 | 0 | C2v |
| 90 | Disphenocingulum | Datei:Disphenocingulum.png | 16 | 38 | 24 | 20 | 4 | 0 | 0 | D2d |
| 91 | Bilunadoppelrotunde | Datei:Bilunabirotunda.png | 14 | 26 | 14 | 8 | 2 | 4 | 0 | D2h |
| 92 | Dreieckshebosphenorotunde | Datei:Triangular hebesphenorotunda.png | 18 | 36 | 20 | 13 | 3 | 3 | 1 | C3v |
Literatur und Links
- ↑ Norman W. Johnson: Convex Solids with Regular Faces. In: Canadian Journal of Mathematics. Bd. 18, 1966, ISSN 0008-414x, S. 169–200.
- ↑ Viktor A. Zalgaller: Convex Polyhedra with Regular Faces (= Seminars in Mathematics. Bd. 2, ISSN 0080-8873). Consultants Bureauvon, New York NY 1969.
- Eric W. Weisstein: Johnson Solid. In: MathWorld. (englisch)
- Johnson Solid (mit diversen Grafiken, engl.)