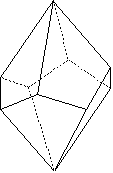
Trapezoeder

Ein Trapezoeder ist ein Polyeder, das von deckungsgleichen „schiefen“ Vierecken begrenzt ist – also von solchen, bei denen keine Seite einer anderen parallel ist (Trapezoide oder Trapeze im älteren Sinn^[1]). Ein Trapezoeder im engeren Sinn kann man sich als eine Bipyramide vorstellen, bei der die obere gegen die untere Pyramide um einen beliebigen Winkel verdreht ist.

Trapezoeder kommen in der Natur als Kristallform vor: Sie sind die allgemeine Flächenform der enantiomorphen Kristallklassen 32 (trigonal-trapezoedrische), 422 (tetragonal-trapezoedrische) und 622 (hexagonal-trapezoedrische Klasse).

Ein Trapezoeder mit höherer Symmetrie entsteht, wenn die Flächen der oberen Pyramide genau in der Mitte zwischen denen der unteren liegen. Der Winkel der Verdrehung ist dann 180°/m bei einer m-zähligen Pyramide. Die Flächen solcher Körper sind Deltoide („Drachen“). Diese höhersymmetrischen Trapezoeder werden auch Deltoeder oder Antipyramide genannt.

• 

  trigonales Trapezoeder

• 

  tetragonales Trapezoeder

• 

  pentagonales Trapezoeder als zehnseitiger Spielwürfel

• 

  hexagonales Trapezoeder

Daneben wird gelegentlich auch das kubische Deltoidalikositetraeder, ein Körper mit 24 drachenförmigen Flächen, Trapezoeder genannt.

Einzelnachweise

Weblinks

• Eric W. Weisstein: Trapezohedron. In: MathWorld. (englisch)