Quantengatter
- Seiten mit defekten Dateilinks
- Quanteninformatik
Quantengatter sind die elementaren Operationen, die ein Quantencomputer auf seinen Qubits durchführen kann. Sie sind vergleichbar mit elektronischen Gattern, welche die elementaren Operationen eines klassischen Computers durchführen. Ein Quantengatter arbeitet jedoch mit quantenmechanischen Systemen wie dem Spin. Auch wenn ihr Name es suggeriert, stellen Quantengatter in der Regel keine physikalischen Bauelemente wie Transistoren dar. Ein Quantengatter ist vielmehr eine zeitlich steuerbare Wechselwirkung der Qubits untereinander oder mit der Umgebung.
Aus mathematischer Sicht ist ein Quantengatter eine unitäre Transformation $ U $, welche auf den Zustand $ \Psi $ der Qubits angewendet wird und den Zustand $ U\Psi $ erzeugt. Die Unitarität dieser Transformation folgt aus der Forderung, dass ein Quantengatter die Normierung der Wellenfunktion erhalten muss: $ |U\Psi |^{2}=|\Psi |^{2} $.
Darstellung
Um $ U $ als Matrix schreiben zu können, wählt man als Basiszustände üblicherweise gerade die Qubit-Zustände, die klassischen Zahlen entsprechen, für zwei Qubits also
$ |00\rangle ,|01\rangle ,|10\rangle ,|11\rangle . $
Ein Quantengatter, das einfach die beiden Qubits miteinander vertauscht, hätte dann die Matrixdarstellung
$ {\mathsf {SWAP}}={\begin{pmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\end{pmatrix}} $
Für konkrete Berechnungen ist eine solche Matrixdarstellung nützlich. Um aber bei mehreren nacheinander auf das System angewendeten Quantengatter nicht die Übersicht zu verlieren, führt man analog zu den klassischen Logikgattern Schaltsymbole ein, die zu einem Quantenschaltkreis verbunden werden. Jedes Schaltsymbol entspricht darin einer unitären Operation.
Die gezeigten Graphen sollen die Bloch-Kugel für verschiedene Anfangs- und Endzustände darstellen, welche jeweils in einer anderen Farbe dargestellt sind. Dadurch kann man sich die Drehungen besser vorstellen. Die Wahrscheinlichkeiten der einzelnen überlagerten Zustände können in dieser Darstellungsform allerdings nicht berücksichtigt werden.
Universelle Gates
Aus Gründen der einfacheren Realisierung ist es wünschenswert, sich bei einem Quantencomputer ähnlich wie beim klassischen Computer auf eine handvoll elementarer, einfach zu realisierender Gatter zu beschränken. Dort ist beispielsweise das NAND-Gatter alleine ausreichend, um jeden denkbaren Schaltkreis zu bauen.
Eine Menge von Quantengattern wird universell genannt, wenn sich jede unitäre Transformation $ U $ als Produkt von Gattern aus der betrachteten Menge darstellen lässt.
Es konnte gezeigt werden, dass das CNOT-Gatter zusammen mit allen 1-Qubit-Gattern eine solche universelle Menge ist.
Beispiele
| Name | Matrix | Symbol | Beschreibung |
|---|---|---|---|
| Hadamard-Gatter | $ {\frac {1}{\sqrt {2}}}{\begin{pmatrix}1&1\\1&-1\end{pmatrix}} $ | Hadamard-Gatter | Überführt $ |0\rangle $ und $ |1\rangle $ in überlagerte Zustände. |
| Controlled-NOT (CNOT) | $ {\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{pmatrix}} $ | 
|
Das erste Qubit wird Kontroll-Qubit bezeichnet, das zweite Ziel-Qubit. Das Ziel-Qubit wird invertiert genau dann, wenn das Kontroll-Bit auf $ |1\rangle $ ist. |
Besonderheiten
Quantengatter weisen neben den zu Beginn genannten Eigenschaften noch weitere Besonderheiten auf, die sie von den klassischen Gattern unterscheiden und daher noch einmal betont werden sollen.
Umkehrbarkeit
Die vom Quantengatter realisierte Operation ist eine unitäre Transformation und damit insbesondere auch eine umkehrbare oder reversible Transformation. Das bedeutet: Die Wirkung von jedem Quantengatter kann mit einem anderen Quantengatter rückgängig gemacht werden. Eine Folge davon ist, dass ein Quantengatter nicht mehr Eingänge als Ausgänge haben kann, denn dann würde ja eines der Eingangsqubits verloren gehen.
Nicht-Kopierbarkeit
Da ein Quantengatter eine auf den Qubits durchgeführte Operation ist, kann ein Quantengatter nicht mehr Qubits erzeugen, als von Anfang an vorhanden sind. Insbesondere lässt sich der Zustand eines Qubits nicht kopieren, ohne den Ausgangszustand zu zerstören. Dies besagt das wichtige No-Cloning-Theorem. Während also in einem klassischen Schaltplan die Leitung von einem Bit in zwei Leitungen verzweigen kann, ist dies beim Quantencomputer nicht möglich.
Daher gibt es in einem Quantenschaltkreis genau eine Leitung pro Qubit. Diese wird durchgehend von links nach rechts durch den Schaltplan gezeichnet und beinhaltet die 1-Qubit-Gatter sowie die Anschlüsse der Mehr-Qubit-Gatter.
Realisierung
Die physikalische Realisierung eines Quantengatters hängt selbstverständlich davon ab, wie das Qubit selbst physikalisch realisiert wird. In einer Ionenfalle festgehaltene Teilchen werden beispielsweise mit Hilfe von Photonen mit einem vorgegebenen Quantisierungszustand manipuliert.
| Schritt 1 | Schritt 2 | Schritt 3 |
|---|---|---|
|
|
|
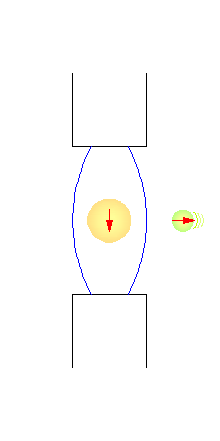
| Ein Ion (gelb) wird in einer Ionenfalle durch ein elektromagnetisches Feld (blau) festgehalten und durch einen Laser gekühlt. Auf dieses Ion wird ein polarisiertes Photon (grün) "geschossen". | Sobald das Photon auf das Ion trifft, entsteht eine Wechselwirkung zwischen den beiden Teilchen. Dies ist die eigentliche Rechenoperation an dem Quantensystem. | Wenn das Photon die Ionenfalle verlässt, hat das Ion einen Zustand eingenommen, der sich aus der Überlagerung des Quantenzustandes des Ions und des Photons ergibt. |
1-Qubit Gatter
Ein einzelnes Qubit mit den Zuständen $ |0\rangle ,|1\rangle $ kann rein formal stets als Spin-Zustand eines Spin-½-Teilchens geschrieben werden. Die Zustände können daher stets als Elemente auf der so genannten Bloch-Kugel dargestellt werden. Ein Gatter, welches auf einem einzelnen Qubit arbeitet, kann dann formal als Rotation auf der Bloch-Kugel um einen bestimmten Winkel beschrieben werden.
2-Qubit Gatter
Für Quantengatter, die auf zwei Qubits arbeiten, ist eine Wechselwirkung zwischen den fraglichen Qubits erforderlich. Bei Spin-Qubits kann dies unter anderem über die Austauschwechselwirkung geschehen. Atome in einer Ionenfalle könnten Photonen austauschen.
Da Gatter mit mehr als zwei Eingängen zwar theoretisch denkbar sind, aber auf Grund der dafür nötigen Mehrteilcheneffekte wesentlich komplexer umzusetzen sind, beschränkt man sich bei Vorschlägen für Quantencomputer in der Regel auf die 1- und 2-Qubit-Gatter. Es genügt ja, mit diesen Gattern eine universelle Menge von Gattern zu haben.
siehe auch: Liste der Quantengatter, Optimal Quantum Circuits for General Two-Qubit Gates
Wirkung
Quantengatter mit einem einzigen Eingang sind in der Lage ein einzelnes Qubit zu verändern. Dieses Qubit kann lediglich entweder logisch 1 oder logisch 0 darstellen. Das allein ist also kein Vorteil im Vergleich zu den bisherigen elektronischen Gattern. Die Phasenlage ist jedoch ein Indikator dafür, wie wahrscheinlich die jeweiligen Zustände sind. Man spricht hierbei davon, dass sich die beiden Zustände $ \left|0\right\rangle $ und $ \left|1\right\rangle $ überlagern und sich das Qubit in Superposition befindet. Beispielsweise sind bei einer Phasenverschiebung von 90° die Messwerte zu 50 % logisch 1 und die anderen 50 % der Messwerte logisch 0. Eine Rechenoperation auf ein solches Qubit wird daher auf den Zustand $ \left|0\right\rangle $ und den Zustand $ \left|1\right\rangle $ gleichzeitig angewendet.
Der Nachteil ist, dass bei einer Messung aufgrund des Kollaps der Wellenfunktion nur ein einzelnes mögliches Ergebnis zurückgeliefert wird. Ein brauchbares Ergebnis ist daher meistens nur durch mehrfaches Wiederholen der Rechenoperation und eine anschließende statistische Auswertung der Messergebnisse möglich. Wenn jedoch mit mehreren Qubits gleichzeitig gerechnet wird, kann man manchmal mit einem Trick, zum Beispiel der Quanten-Fouriertransformation, schon mit nur einer Berechnung an brauchbare Ergebnisse kommen.