Hysterese

Hysterese, auch Hysteresis (griech. hysteros „hinterher, später“), charakterisiert ein Systemverhalten, bei dem die Ausgangsgröße nicht allein von der unabhängig veränderlichen Eingangsgröße abhängt, sondern auch von dem vorherigen Zustand der Ausgangsgröße. Das System kann – abhängig von der Vorgeschichte – bei gleicher Eingangsgröße mehrere Zustände einnehmen.

Dieses Verhalten ist entweder für das Material typisch (Ferromagnetismus) oder wird beispielsweise beim Zweipunktregler oder beim Dreipunktregler eingeprägt. Das System zeigt dabei Pfadabhängigkeit.

Hysterese tritt bei vielen natürlichen und technischen Vorgängen und Regelungsprozessen auf und ist damit ein wesentlicher Begriff der Regelungstechnik und der Kybernetik. Der Ausdruck Hysteresis wurde von Sir James Alfred Ewing geprägt.

Hysterese-Effekte

Magnetische Hysterese

→ Hauptartikel: Ferromagnetismus#Hysterese

Ein Hystereseverhalten tritt bei ferromagnetischen Stoffen wie Eisen, Kobalt und Nickel auf. Die magnetische Flussdichte in einem ferromagnetischen Stoff wird von der Stärke des umgebenden Magnetfeldes ( $$ H $$ ) bestimmt. Geht das äußere Magnetfeld zurück, so nimmt die Flussdichte wieder ab. Die magnetische Flussdichte erreicht bei dem gleichen Wert einer Feldstärke, die im Abnehmen begriffen ist, einen höheren Wert als er während des Zunehmens der Feldstärke auftrat. Ein Umkehren (negativer Wert) der Feldstärke von $$ H $$ führt dazu, dass der obere Ast der Hysteresekurve durchlaufen wird. Dieser Hysteresevorgang lässt sich gut am Verlauf der Magnetisierungskurve, Hysteresekurve oder Hystereseschleife verdeutlichen. Ein vollständiges Durchlaufen der Hysteresekurve wird als Hysteresezyklus bezeichnet.

Hystereseverluste

Wenn Materialien ummagnetisiert werden, muss Energie für die veränderte Ausrichtung der Weiss-Bezirke aufgewendet werden. Dieses Drehen verursacht Wärme im Eisen. Die Verluste sind im Allgemeinen proportional zu der Fläche innerhalb der Hysteresekurve.

Weitere Beispiele

Technik

Werkstofftechnik: Das elastisch-plastische Verformungsverhalten eines Werkstoffs unterliegt einer Hysterese. Bei der Auftragung im Spannungs-Dehnungs-Diagramm erhält man eine Hystereseschleife.
Kybernetik und Regelungstechnik: Zweipunktregler besitzen immanent ein Hysterese-Verhalten.
Logikschaltungen / Interfaces: Schmitt-Trigger sind Schwellenwertschalter und erzeugen aus langsam ablaufenden Vorgängen exakte Logiksignale
Messtechnik: die Umkehrspanne von Zeigerinstrumenten wird auch Hysterese genannt. Sie rührt von mechanischen Ungenauigkeiten wie Spiel und oder Reibung zum Beispiel in Lagern der Messgeräte her.
Hysterese bei Lageregelungen: Ein Servomotor arbeitet z. B. als Aktor in mechanischen Regelkreisen, z. B. bei dem Ruder eines Flugzeugs. Er erzeugt bzw. hält dann einen bestimmten Stellwinkel, und steuert dazu auch gegen äußere Kräfte (wie Turbulenzen) per Soll-Ist-Vergleich. Um Regelschwingungen aufgrund mechanischen Spieles (permanentes, alternierendes Gegensteuern kleinster Abweichungen, Flattern) zu vermeiden, ist eine Hysterese im Regelkreis notwendig. Dazu wird, abhängig von der Genauigkeit der Ist-Sensoren und der mechanischen Präzision, eine verzögerte Reaktion auf eine Sollabweichung konstruiert bzw. programmiert.
Hysterese bei Herzschrittmacher-Reglern: Herzschrittmacher besitzen ein hysteresebehaftetes Ansprechverhalten. Üblicherweise wird eine bestimmte Interventionsfrequenz („Bedarfsfrequenz“) programmiert, z. B. 60 Schläge pro Minute. Der Schrittmacher greift normalerweise ein, sobald die Pulsfrequenz des Patienten unter die Bedarfsfrequenz abfällt und stimuliert den Sinusknoten mit 60 Impulsen pro Minute. Programmiert man dagegen die Hysteresefunktion, so springt der Schrittmacher erst bei einer tieferen Frequenz (z. B. 50 min⁻¹) ein, stimuliert dann aber mit der Interventionsfrequenz (z. B. 60 min⁻¹).
Rheologie: Beim Fließverhalten von nicht-newtonschen thixotropen Fluiden wird ebenfalls von Hysterese gesprochen. Dabei ist die Änderung der Viskosität, d. h. die Verringerung der Zähigkeit eines solchen Fluids unter Einfluss eines konstanten Schergradienten, abhängig von der Dauer der Einwirkung. Mit Zunahme der Dauer der Einwirkung durch die Scherung ist der Hystereseeffekt zunehmend irreversibel.

Die Physik kennt drei Formen der Dämpfung, d. h. drei verschiedene Vorgänge, die im Werkstoff ablaufen können und zur Ausbildung einer Verlustschleife führen. Kriechen führt zu Relaxationsvorgängen, die eine dieser drei Formen bilden (Relaxationsdämpfung). Charakteristisch für solche Prozesse ist die Unabhängigkeit der Dämpfung von der Amplitude und die Abhängigkeit von der Frequenz des Eingangssignals. Für beide Enden des Frequenzintervalls hat die Dämpfung den Wert Null. Gleiches gilt für die Resonanzdämpfung. Sie unterscheidet sich von der Relaxationsdämpfung dadurch, dass für die Resonanzfrequenz der dynamische Modul kleiner wird als für alle anderen Frequenzen. Im Gegensatz dazu sind Dämpfung und Modul bei der Hysterese frequenzunabhängig, aber i. Allg. amplitudenabhängig.

Schifffahrt: Hier bezeichnet Hysterese die Erscheinung, dass eine Gierbewegung bei einer Änderung des Ruder-Ausschlages bzw. Ruder-Winkels zunächst unverändert anhält, bevor sie dem Ruderausschlag folgt.
Bei Flüssigkristallen verlaufen Phasenänderungen in Form einer Hysteresekurve.
Ferroelektrika besitzen ein der magnetischen Hysterese analoges elektrisches Hystereseverhalten
Im Mobilfunk wird beim Hand-off Prozess zwischen zwei Basisstationen ebenfalls eine Hysterese angewendet. Die Besonderheit ist hier, dass der Hysterese ein Wert zugeordnet wird: Ein mobiler Teilnehmer soll die Basisstation wechseln, wenn das Sendesignal der aktuellen Basisstation schlechter ist als −55 dBm, mit einer Hysterese von 5 dB. Dies bedeutet, dass der Teilnehmer nur zu Basisstationen wechselt, die mit mindestens −50 dBm oder besser empfangen werden.
Bodenphysik: Bei der Aufsättigung und Entwässerung von Böden ist die Beziehung zwischen Porenwasserdruck (Saugspannung) und Sättigungsgrad (oder Wassergehalt) hysteretisch. Hierdurch können sich zu einem Wassergehalt unterschiedliche Saugspannungen einstellen und umgekehrt. Vielfach ist bei einem Drainagevorgang bei gleicher Saugspannung der Wassergehalt höher als beim Benetzungsvorgang. Eine Erklärung liefert die Porenstruktur natürlicher Böden mit ihrer weiten Porengrößenverteilung. Beim Drainagevorgang werden große Poren, die von kleineren umgeben sind, erst entleert, wenn die Saugspannung die kleinen Poren zu entwässern vermag. Umgekehrt verhindern große Poren die Benetzung angrenzender kleiner Poren, bis die Saugspannung erreicht ist, die auch die großen Poren benetzen kann. Gemäß diesem Modell scheint Hysterese vor allem im Sandboden aufzutreten, während im Lehm kein signifikanter Effekt festgestellt werden konnte.

Wirtschaftswissenschaften

In den Wirtschaftswissenschaften, etwa der Volkswirtschaftslehre, bezeichnet Hysterese etwa die Reaktion eines Marktes auf externe Einflüsse, nach deren Abklingen ein (Preis-) System nicht mehr in seinen Ausgangszustand zurückkehrt.

Siehe Hauptartikel: Hysterese (Wirtschaftswissenschaft)

Mathematik

In dynamischen Systemen bezeichnet die Hysterese ein Phänomen der Rückwärts-Bifurkation.

Physiologie

Ruhedehnungskurve der Lunge

In der Physiologie ist eine Hysterese u. a. in der Ruhedehnungskurve der Lunge zu finden. Damit bezeichnet man den Umstand, dass das Volumen der Lunge bei einer Abnahme des intrapulmonalen Drucks langsamer abnimmt, als es bei einer Druckerhöhung zugenommen hat.

Der Grund dafür ist in der Reorganisation der Moleküle des Surfactant-Faktors während des Atemzyklus zu sehen.

Thermische Hystereseproteine (THP) führen bei Tieren, z. B. Fischen zu einem Gefrierschutz. Wenn verstärkt THP in der Körperflüssigkeit vorliegen, kommt es zu einer thermischen Hysterese bei der Eisbildung. Die Körperflüssigkeit gefriert bspw. bei −5 °C, taut allerdings erst bei 0 °C wieder auf. Dieses geschieht nicht durch eine Erhöhung der Molarität in der Extrazellulärflüssigkeit, sondern dadurch, dass die Bindung der THP an die Eiskristalle eine weitere Eisbildung verhindert.

Beispiele zur Erklärung

„Harte“ Hysterese beim Zweipunktregler

Der Zweipunktregler ist ein typisches Beispiel. In der grafischen Darstellung wird die Ursache (Eingangsgröße) meistens auf einer horizontalen Achse aufgetragen, die Wirkung (Ausgangsgröße) auf der vertikalen Achse.

Als Beispiel dient das Ausklappen des Heckspoilers bei einem Auto: Diese „Luftklappe“ soll bei geringen Geschwindigkeit eingefahren und oberhalb von 80 km/h ausgefahren sein, um den Anpressdruck der Hinterräder zu erhöhen. Wenn das Auto in einer Kolonne fährt, deren Geschwindigkeit ständig zwischen 78 km/h und 83 km/h schwankt, würde das ständige Ein- und Ausfahren die Spoiler-Mechanik unnötigerweise beanspruchen. Das wird durch ein hysteresebehaftetes Schaltverhalten vermieden. Im nebenstehenden Bild ist die Ursache – die Geschwindigkeit – auf der horizontalen Achse aufgetragen und die beiden Umschaltpunkte für den Zweipunktregler festgelegt:

Oberhalb von 80 km/h wird ausgefahren, obere Linie auf der Hysteresekurve.
Unterhalb von 60 km/h wird eingefahren, untere Linie auf der Hysteresekurve.

Auf der senkrechten Achse wird die zugehörige Spoilerstellung markiert.

Der Zustand des Heckspoilers bei den zwischen den Schaltpunkten liegenden Geschwindigkeiten kann an der vertikalen Achse abgelesen werden und hängt von der Geschwindigkeits-Vorgeschichte ab, also von welcher Richtung aus im Bild die Geschwindigkeit auf die Hysteresekurve zuläuft:

War das Auto vorher schneller, bleibt er ausgefahren, bis das Auto langsamer als 60 km/h fährt.
War das Auto vorher langsamer, bleibt er eingefahren, bis das Auto schneller als 80 km/h fährt.

Harte und weiche Hysteresekurve

Harte Hysteresekurve mit Zwischenzuständen mit hoher Remanenz bei hoher Koerzitivfeldstärke

Weiche Hysteresekurve von einem EI-Transformator-Eisenkern mit Luftspalt und kleiner Remanenz bei kleiner Koerzitivfeldstärke

Harte Hysteresekurve eines Transformator-Eisenkerns ohne Luftspalt (Ringkern) mit hoher Remanenz bei kleiner Koerzitivfeldstärke

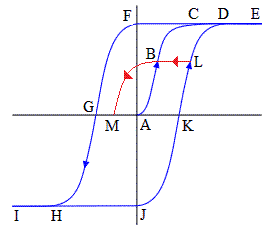
Die harte und weiche Hysterese wird im folgenden am Magnetismus erklärt. Die drei Bilder zeigen Hysteresekurven von einem Dauermagneten mit harter Hysteresekurve, der eine hohe Koerzitivfeldstärke und eine hohe Remanenz besitzt und Transformator-Eisenkernen (siehe auch: Dynamoblech), die eine kleine Koerzitivfeldstärke und unterschiedliche starke Neigungen, Scherung, und Remanenzen besitzen und weiche und harte Hysteresekurven darstellen die jedoch im Gegensatz zu einem Dauermagnetischen Material eine kleine Koerzitivfeldstärke haben.

Ein einzelner Weiss-Bezirk eines ferromagnetischen Stoffes besitzt eine steile, in der Mitte fast senkrecht verlaufende, harte Hysteresekurve mit bistabilem Verhalten – ein Effekt, der in den jungen Jahren der Computertechnik zum Speichern von Bits in einem Kernspeicher verwendet wurde. Bei Ferromagnetismus in einem rechteckigen, ausgestanzten Trafoblech liegen diese weissschen Bezirke zwar in der Walzrichtung des Ausgangsbleches, aber zum Beispiel bei einem M-Schnitt nur in zwei Schenkeln günstig zur Magnetfeldrichtung. Weil der Magnetfluss jedoch auch durch Schenkel laufen muss, bei denen die Orientierung der Weisschen Bezirke nicht in Magnetflussrichtung liegt und die deshalb eine geneigte Kurve haben, gibt es eine Gesamtsumme von Millionen „Schaltern“ (Weiss-Bezirken), die sich in ihrer Orientierung zur Magnetfeldrichtung voneinander unterscheiden. Die Summe aller dieser fast senkrechten und geneigten Hysteresekurven ist die „weiche“ und geneigte Hysteresekurve im Bild in der Mitte rechts. Bei einem Ringkerntransformator dagegen liegt die Orientierung aller weissschen Bezirke durch das Walzen in Magnetflussrichtung, was eine steil verlaufende, harte (Gesamt-)Hysteresekurve ergibt. Die Ummagnetisierungsenergie ist hierbei am kleinsten, was auch der kleinsten Fläche innerhalb der Hysteresekurve entspricht. Man spricht deshalb dann von harten Rechteckkernen mit einer steil verlaufenden Hysteresekurve, die jedoch ebenfalls wie die Weiche Kurve, kurz vor der Kernsättigung mit einem Bogen, in die fast Waagerechte abbiegt. Dabei gibt es – abhängig von der Anzahl der in Magnetflussrichtung orientierten, weissschen Bezirke im Verhältnis zu den quer dazu liegenden,– besondere Phänomene:

Nur wenn das Eisenstück entmagnetisiert war, ist der Startpunkt bei A. Das blaue Kurvenstück von A über B nach C heißt auch „jungfräuliche“ Kurve oder "Neukurve".
Man kann mit einem Elektromagneten bis zum Punkt B in einer Richtung magnetisieren und dann – nach Umpolen des Elektromagneten – auf der roten Kurve bis zum Punkt M gehen. Dann wurden nur wenige Weiss-Bezirke in ihrer Orientierung geändert. Der vertikale Abstand zur horizontalen Achse, gibt an, wie viele Bezirke beeinflusst wurden. Er sagt etwas über die Flussdichte aus.
Man kann auch von A bis C oder bis D oder bis E gehen – das hängt davon ab, wie stark der Elektromagnet ist. Zwischen C und E sind alle Weiss-Bezirke parallel orientiert, dann spricht man von Sättigung. Eine weitere Erhöhung des Spulenstromes verstärkt nur noch unwesentlich den magnetischen Fluss im Eisen.
Wenn der Elektromagnet abgeschaltet wird, gelangt man zurück bis F. Ob F genauso hoch liegt wie C oder schon ein wenig oder sogar viel tiefer, hängt von der Remanenz ab. Diese ist von der Bauform, u. a. vom (Rest)Luftspalt abhängig.
Polt man den Elektromagneten um und erhöht langsam die Spannungszeitfläche, gelang man zum Punkt G. Das Eisenstück ist entmagnetisiert worden, solange das Gegenfeld anliegt. Dazu musste die Koerzitivfeldstärke des Kernes im Elektromagneten überwunden werden. Nach dem Ausschalten des Gegenfeldes läuft die Magnetisierung wie eine elastische Feder wieder auf den vorigen Wert F. Zum Nullpunkt A gelangt man nur, wenn man die Aussteuerung der Hysteresekurve in kleinen Schritten oder kontinuierlich, durch ein sich ständig umpolendes und kleiner werdendes Gegenfeld verkleinert (Entmagnetisierung).

Siehe auch

Hysterese bei Zellstoff

Literatur

J. Möller, R. Völker: Lohnbildung und Hysteresis: Empirische Überprüfung eines Insider-Outsider Modells für die Bundesrepublik Deutschland. In: Zeitschrift für Wirtschafts-und Sozialwissenschaften. 111, 1991, S. 401–424.
A. Belke, M. Göcke: Starke Hysteresis auf dem Arbeitsmarkt. In: ZWS-Zeitschrift für Wirtschafts- und Sozialwissenschaften. 114, 1994, S. 345–377.

Weblinks