Rektaszension
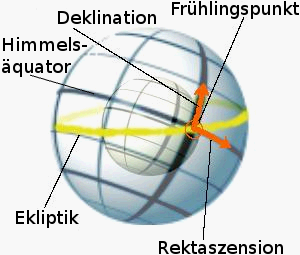
Die Rektaszension (lat. ascensio recta = gerader Aufstieg) ist eine der beiden Polarkoordinaten im sogenannten rotierenden äquatorialen Koordinatensystem der sphärischen Astronomie.[1] Dessen zweite Koordinate ist die Deklination.
Sie ist der auf den Himmelsäquator bezogene Winkel zwischen dem Frühlingspunkt und dem Längenkreis, auf dem der beobachtete Himmelskörper steht, und ist das Analogon zur sich auf die Erdkugel beziehenden geographischen Länge. Die gebräuchlichsten Abkürzungen sind α oder a.
Die Rektaszension wird häufiger im Zeitmaß als in Grad oder Bogenmaß angegeben. Die Angabe im Zeitmaß nimmt Bezug darauf, dass die scheinbare Rotation der Sterne um die Erde zur Zeit proportional ist und Zeitdifferenzen relativ einfach bestimmt werden können.
Wortbedeutung und Zeitmaß
Das Wort Rektaszension ist die Zusammenschreibung von recta ascension, der umgekehrten Reihenfolge des lateinischen ascensio recta. Im Englischen wird der Begriff right ascension (gebräuchliche Abkürzung RA) als wörtliche Übersetzung des alten lateinischen Begriffs verwendet. In der älteren deutschsprachigen Literatur wurde ebenfalls die wörtliche Übersetzung aus dem Lateinischen benutzt, nämlich gerader Aufstieg oder Geradeaufsteigung.[2].
Ascensio recta bezieht sich darauf, wie der Aufstieg (ascensio, ascension oder Aufstieg) eines Sterns über den Horizont am Erdäquator erfolgt, nämlich rechtwinklig (recta, right oder gerade) zum Horizont. Im Moment des Sternaufgangs fällt dessen Längenkreis mit dem Horizontkreis zusammen. Der Ostpunkt des Horizonts ist der Schnittpunkt des Längenkreises mit dem dort vertikal verlaufenden Himmelsäquator und damit der momentane Punkt, bis zu dem die Rektaszension des Sternes zu messen ist.[3]
Wenn ein Stern am Äquator eine Stern-Stunde nach dem Frühlingspunkt aufgeht, so hat er die Rektaszension 15° (in einem Stern-Tag zu 24 Stern-Stunden bewegen sich die Sterne scheinbar auf einem vollen Kreis mit 360°).
Äquatoriales Koordinatensystem

Als Nullpunkt der Rektaszension dient der Frühlingspunkt. Sie wächst wie die geografische Länge gegen Osten.
In der astronomischen Navigation wird statt der Rektaszension auch der sich nach Westen vergrößernde Sternwinkel (engl. sidereal hour angle (SHA)) verwendet.
Im ortsfesten äquatorialen Koordinatensystem wird statt der Rektaszension der Stundenwinkel verwendet.
Rektaszension α und Deklination δ entsprechen im ekliptikalen Koordinatensystem die ekliptikale Länge λ und die ekliptikale Breite β. Zur Umrechnung wird die Ekliptikschiefe ε gebraucht, siehe kleines Dreieck rechts auf der Skizze. Diese Koordinatentransformation ist für die Berechnung der Umlaufbahnen von Planeten und anderer Körper des Sonnensystems unerlässlich.
Einzelnachweise
- ↑ Für den Beobachter auf der Erde rotiert der Bezugspunkt Frühlingspunkt auf dem Himmelsäquator.
- ↑ Friedrich Wilhelm Bessel: Astronomische Untersuchungen. Band 2, Königsberg 1842, Seite 107 (online)
- ↑ John Lathrop (1821): A Compendious Treatise on the Use of Globes and Maps S. 39 (187.). Wells and Lilly and J.W. Burditt, Boston. Abgerufen am 11. Juni 2012.
Weblinks
- Rektaszension – der himmlische Längengrad – Seite bei BR-online