Differentialrechnung

Die Differential- bzw. Differenzialrechnung ist ein wesentlicher Bestandteil der Analysis und damit ein Gebiet der Mathematik. Sie ist eng verwandt mit der Integralrechnung, mit der sie unter der Bezeichnung Infinitesimalrechnung zusammengefasst wird. Zentrales Thema der Differentialrechnung ist die Berechnung lokaler Veränderungen von Funktionen.

Hierzu dienlich und gleichzeitig Grundbegriff der Differentialrechnung ist die Ableitung einer Funktion (auch Differentialquotient genannt), deren geometrische Entsprechung die Tangentensteigung ist. Die Ableitung ist (nach der Vorstellung von Leibniz) der Proportionalitätsfaktor zwischen verschwindend kleinen (infinitesimalen) Änderungen des Eingabewertes und den daraus resultierenden, ebenfalls infinitesimalen Änderungen des Funktionswertes. Existiert ein solcher Proportionalitätsfaktor, so nennt man die Funktion differenzierbar. Äquivalent wird die Ableitung in einem Punkt als diejenige lineare Abbildung definiert, die unter allen linearen Abbildungen die Änderung der Funktion lokal am besten approximiert. Entsprechend wird die Ableitung auch die Linearisierung der Funktion genannt.

In vielen Fällen ist die Differentialrechnung ein unverzichtbares Hilfsmittel zur Bildung von mathematischen Modellen, die versuchen die Wirklichkeit abzubilden, sowie zu deren nachfolgender Analyse. Die Entsprechung der Ableitung im untersuchten Sachverhalt ist häufig die momentane Änderungsrate; in den Wirtschaftswissenschaften spricht man auch häufig von Grenzraten (z. B. Grenzkosten, Grenzproduktivität eines Produktionsfaktors etc.).

Dieser Artikel erklärt außerdem die mathematischen Begriffe: Differenzenquotient, Differentialquotient, Differentiation, stetig differenzierbar, glatt, partielle Ableitung, totale Ableitung, Reduktion des Grades eines Polynoms.

In geometrischer Sprache ist die Ableitung eine verallgemeinerte Steigung. Der geometrische Begriff Steigung ist ursprünglich nur für lineare Funktionen definiert, deren Funktionsgraph eine Gerade ist. Die Ableitung einer beliebigen Funktion an einer Stelle $ x_{0} $ definiert man als die Steigung der Tangenten im Punkt $ (x_{0};f(x_{0})) $ des Graphen von $ f $.

In arithmetischer Sprache gibt die Ableitung einer Funktion $ f $ für jedes $ x $ an, wie groß der lineare Anteil der Änderung von $ f(x) $ ist (die Änderung 1. Ordnung), wenn sich $ x $ um einen beliebig kleinen Betrag $ \Delta x $ ändert. Für die exakte Formulierung dieses Sachverhalts wird der Begriff Grenzwert (oder Limes) verwendet.

In einer klassischen physikalischen Anwendung liefert die Ableitung der Orts- oder Weg-Zeit-Funktion nach der Zeit die Momentangeschwindigkeit eines Teilchens.

Geschichte

Die Aufgabenstellung der Differentialrechnung war als Tangentenproblem seit der Antike bekannt. Ein nahe liegender Lösungsansatz bestand darin, die Tangente an eine Kurve durch ihre Sekante über einem endlichen (endlich heißt hier: größer als null), aber beliebig kleinen Intervall zu approximieren. Dabei war die technische Schwierigkeit zu überwinden, mit einer solchen infinitesimal kleinen Intervallbreite zu rechnen. Dies gelang Pierre de Fermat um 1640 für das Tangentenproblem bei Polynomen. Er formulierte bereits eine Ableitung, jedoch ohne dabei Grenzwerte zu betrachten und ohne eine mathematische Begründung für sein Vorgehen niederzuschreiben. Zur selben Zeit wählte René Descartes einen algebraischen Zugang, indem er an eine Kurve einen Kreis anlegte. Dieser schneidet die Kurve in zwei nahe beieinanderliegenden Punkten, es sei denn er berührt die Kurve. Dieser Ansatz ermöglichte es ihm für spezielle Kurven die Steigung der Tangente zu bestimmen.

Ende des 17. Jahrhunderts gelang es Isaac Newton und Gottfried Wilhelm Leibniz unabhängig voneinander, widerspruchsfrei funktionierende Kalküle zu entwickeln (zur Entdeckungsgeschichte und zum Prioritätsstreit siehe den Artikel Infinitesimalrechnung). Newton ging das Problem jedoch von einer anderen Seite an als Leibniz. Während Newton das Problem physikalisch über das Momentangeschwindigkeitsproblem anging, versuchte es Leibniz geometrisch über das Tangentenproblem. Ihre Arbeiten erlaubten das Abstrahieren von rein geometrischer Vorstellung und werden deshalb als Beginn der Analysis betrachtet. Bekannt wurden sie vor allem durch das Buch des Adligen Guillaume François Antoine, Marquis de L’Hospital, der bei Johann Bernoulli Privatunterricht nahm und dessen Forschung zur Analysis so publizierte. Die heute bekannten Ableitungsregeln basieren vor allem auf den Werken von Leonhard Euler, der den Funktionsbegriff prägte. Newton und Leibniz arbeiteten mit beliebig kleinen Zahlen, die aber größer als null sind. Dies wurde bereits von Zeitgenossen als unlogisch kritisiert, beispielsweise von Bischof Berkeley in der polemischen Schrift The analyst: or a discourse addressed to an infidel mathematician. Die Differentialrechnung wurde aber trotz herrschender Unsicherheit konsequent weiterentwickelt; in erster Linie wegen ihrer zahlreichen Anwendungen in der Physik und in anderen Gebieten der Mathematik. Symptomatisch für die damalige Zeit war das von der Preußischen Akademie der Wissenschaften 1784 veröffentlichte Preisausschreiben:

„… Die höhere Geometrie benutzt häufig unendlich große und unendlich kleine Größen; jedoch haben die alten Gelehrten das Unendliche sorgfältig vermieden, und einige berühmte Analysten unserer Zeit bekennen, dass die Wörter unendliche Größe widerspruchsvoll sind. Die Akademie verlangt also, dass man erkläre, wie aus einer widersprechenden Annahme so viele richtige Sätze entstanden sind, und dass man einen sicheren und klaren Grundbegriff angebe, welcher das Unendliche ersetzen dürfte, ohne die Rechnung zu schwierig oder zu lang zu machen …“

Erst zum Anfang des 19. Jahrhunderts gelang es Augustin Louis Cauchy, der Differentialrechnung die heute übliche logische Strenge zu geben, indem er von den infinitesimalen Größen abging und die Ableitung als Grenzwert von Sekantensteigungen („Differenzenquotienten“) definierte. Die heute benutzte Definition des Grenzwerts wurde schließlich von Karl Weierstraß Ende des 19. Jahrhunderts formuliert.

Definition

Einführung

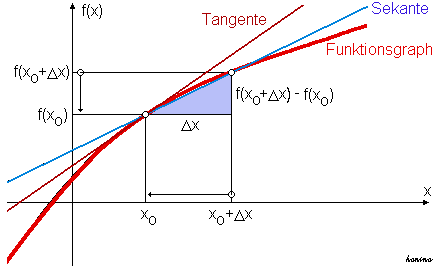
Ausgangspunkt für die Definition der Ableitung ist die Näherung der Tangentensteigung durch eine Sekantensteigung (manchmal auch Sehnensteigung genannt). Gesucht sei die Steigung einer Funktion $ f $ in einem Punkt $ (x_{0}\mid f(x_{0})) $. Man berechnet zunächst die Steigung der Sekante an $ f $ über einem endlichen Intervall:

Sekantensteigung = $ {\frac {f(x_{0}+\Delta x)-f(x_{0})}{(x_{0}+\Delta x)-x_{0}}}={\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}} $.

Die Sekantensteigung ist also der Quotient zweier Differenzen; sie wird deshalb auch Differenzenquotient genannt. Mit der Kurznotation $ \Delta y $ für $ f(x_{0}+\Delta x)-f(x_{0}) $ kann man die Sekantensteigung abgekürzt als $ {\tfrac {\Delta y}{\Delta x}} $ schreiben.

Differenzenquotienten sind aus dem täglichen Leben wohlbekannt, zum Beispiel als Durchschnittsgeschwindigkeit:

„Auf der Fahrt von Augsburg nach Flensburg war ich um 9:43 Uhr ($ x_{0} $) am Kreuz Biebelried (Tageskilometerstand $ f(x_{0}) $ = 198 km). Um 11:04 Uhr ($ x_{0}+\Delta x $) war ich am Dreieck Hattenbach (Tageskilometerstand $ f(x_{0}+\Delta x) $=341 km). In 1 Stunde und 21 Minuten ($ \Delta x $) habe ich somit 143 km ($ \Delta y $) zurückgelegt. Meine Durchschnittsgeschwindigkeit auf dieser Teilstrecke betrug somit 143 km / 1,35 h = 106 km/h ($ \Delta y/\Delta x $).“

Um eine Tangentensteigung (im genannten Anwendungsbeispiel also eine Momentangeschwindigkeit) zu berechnen, muss man die beiden Punkte, durch die die Sekante gezogen wird, immer weiter aneinander rücken. Dabei gehen sowohl $ \Delta x $ als auch $ \Delta y $ gegen Null. Der Quotient $ {\tfrac {\Delta y}{\Delta x}} $ bleibt aber im Normalfall endlich. Auf diesem Grenzübergang beruht die folgende Definition:

Differenzierbarkeit und Ableitung in einem Punkt: Formale Definition und Notation

Eine Funktion $ f\colon U\to \mathbb {R} $, die ein offenes Intervall U in die reellen Zahlen abbildet, heißt differenzierbar an der Stelle $ x_{0}\in U $, falls der Grenzwert

$ \lim _{x\to x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}=\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}} $ (mit $ h=x-x_{0} $)

existiert. Dieser Grenzwert heißt Differentialquotient oder Ableitung von $ f $ nach $ x $ an der Stelle $ x_{0} $ und wird als

$ f'(x_{0}) $ oder $ \left.{\frac {\mathrm {d} f(x)}{\mathrm {d} x}}\right|_{x=x_{0}} $ oder $ {\frac {\mathrm {d} f}{\mathrm {d} x}}(x_{0}) $ oder $ {\frac {\mathrm {d} }{\mathrm {d} x}}f(x_{0}) $ notiert

(gesprochen: „f Strich von x null“, „d f von x nach d x an der Stelle x gleich x null“, „d f nach d x von x null“ respektive „d nach d x von f von x null“).

Die Terme $ \mathrm {d} f $ und $ \mathrm {d} x $ werden als Differentiale bezeichnet, haben aber in der modernen Analysis (zumindest bis zu diesem Punkt der Theorie) lediglich symbolische Bedeutung und sind bisher nur in dieser Schreibweise des formal notierten Differentialquotienten erlaubt. In manchen Anwendungen (Kettenregel, Integration mancher Differentialgleichungen, Integration durch Substitution) rechnet man mit ihnen fast wie mit „normalen“ Variablen. Die präzise formale Begründung hierfür liefert die Theorie der Differentialformen. Ein Differential ist auch Teil der üblichen Notation für Integrale.

Die Notation einer Ableitung als Quotient zweier Differentiale wurde von Leibniz eingeführt. Newton benutzte einen Punkt über der abzuleitenden Größe, was in der Physik für Zeitableitungen bis heute üblich geblieben ist ($ {\dot {x}}(t) $, sprich: „x Punkt“). Die Notation mit Strich ($ f' $) geht auf Joseph-Louis Lagrange zurück, der sie 1797 in seinem Buch Théorie des fonctions analytiques einführte.

Im Laufe der Zeit wurde folgende gleichwertige Definition gefunden, die sich im allgemeineren Kontext komplexer oder mehrdimensionaler Funktionen als leistungsfähiger erwiesen hat:

Eine Funktion heißt in einem Punkt $ x_{0} $ differenzierbar, falls eine Konstante $ L $ existiert, so dass

$ \lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})-Lh}{h}}=0. $

Der Zuwachs der Funktion $ f $, wenn man sich von $ x_{0} $ nur wenig entfernt, etwa um den Wert $ h $, lässt sich also durch $ Lh $ sehr gut approximieren, man nennt die lineare Funktion $ g $ mit $ g(x_{0}+h)=f(x_{0})+Lh $ deswegen auch die Linearisierung von $ f $ an der Stelle $ x_{0} $.

Eine weitere Definition ist: Es gibt eine an der Stelle $ x_{0} $ stetige Funktion $ r $ mit $ r(x_{0})=0 $ und eine Konstante $ L $, so dass für alle $ x $ gilt

$ f(x)=f(x_{0})+L(x-x_{0})+r(x)(x-x_{0}) $.

Die Bedingungen $ r(x_{0})=0 $ und dass $ r $ an der Stelle $ x_{0} $ stetig ist, bedeuten gerade, dass das „Restglied“ $ r(x) $ für $ x $ gegen $ x_{0} $ gegen null konvergiert.

In beiden Fällen ist die Konstante $ L $ eindeutig bestimmt und es gilt $ f'(x_{0})=L $. Der Vorteil dieser Formulierung ist, dass Beweise einfacher zu führen sind, da kein Quotient betrachtet werden muss. Diese Darstellung der besten linearen Approximation wurde schon von Weierstraß, Henri Cartan und Jean Dieudonné konsequent angewandt.

Bezeichnet man eine Funktion als differenzierbar, ohne sich auf eine bestimmte Stelle zu beziehen, dann bedeutet dies die Differenzierbarkeit an jeder Stelle des Definitionsbereiches, also die Existenz einer eindeutigen Tangente für jeden Punkt des Graphen.

Eine differenzierbare Funktion ist immer stetig, die Umkehrung gilt jedoch nicht. Noch Anfang des 19. Jahrhunderts war man überzeugt, dass eine stetige Funktion höchstens an wenigen Stellen nicht differenzierbar sein könne (wie die Betragsfunktion). Bernard Bolzano konstruierte dann als erster Mathematiker tatsächlich eine Funktion, die überall stetig, aber nirgends differenzierbar ist, was in der Fachwelt allerdings nicht bekannt wurde; Karl Weierstraß fand dann in den 1860er Jahren ebenfalls eine derartige Funktion (siehe Weierstraß-Funktion), was diesmal unter Mathematikern Wellen schlug. Ein bekanntes mehrdimensionales Beispiel für eine stetige, nicht differenzierbare Funktion ist die von Helge von Koch 1904 vorgestellte Koch-Kurve.

Ableitung als eine Funktion

Die Ableitung der Funktion $ f $ an der Stelle $ x_{0} $, bezeichnet mit $ f\,'(x_{0}) $, beschreibt lokal das Verhalten der Funktion in der Umgebung der betrachteten Stelle $ x_{0} $. Nun wird $ x_{0} $ im Allgemeinen nicht die einzige Stelle sein, an der $ f $ differenzierbar ist. Man kann daher versuchen, jeder Zahl $ x $ aus dem Definitionsbereich von $ f $ die Ableitung an dieser Stelle (also $ f\,'(x) $) zuzuordnen. Auf diese Weise erhält man eine neue Funktion $ f\,' $, deren Definitionsbereich die Menge $ \Omega $ aller Punkte ist, an denen $ f $ differenzierbar ist. Diese Funktion $ f\,' $ heißt die Ableitungsfunktion oder kurz die Ableitung von $ f $ und man sagt, $ f $ ist auf $ \Omega $ differenzierbar. Beispielsweise hat die Quadratfunktion $ \,f\colon x\mapsto x^{2} $ an einer beliebigen Stelle $ x_{0} $ die Ableitung $ \,f'(x_{0})=2x_{0} $, die Quadratfunktion ist also auf der Menge der reellen Zahlen differenzierbar. Die zugehörige Ableitungsfunktion $ f'\, $ ist gegeben durch $ \,f'\colon x\mapsto 2x $.

Die Ableitungsfunktion ist im Normalfall eine andere als die ursprüngliche, einzige Ausnahme ist neben der Nullfunktion $ f(x)=0 $ die Exponentialfunktion $ e^{x} $ und deren Vielfachen.

Ist die Ableitung stetig, dann heißt $ f $ stetig differenzierbar. In Anlehnung an die Bezeichnung $ C(\Omega ) $ für die Gesamtheit (Raum) der stetigen Funktionen mit Definitionsmenge $ \Omega $ wird der entsprechende Raum der stetig differenzierbaren Funktionen mit $ C^{1}(\Omega ) $ abgekürzt.

Berechnung von Ableitungen

Das Berechnen der Ableitung einer Funktion wird Differentiation genannt; sprich, man differenziert diese Funktion.

Um die Ableitung elementarer Funktionen (z. B. $ x^{n} $, $ \sin(x) $,…) zu berechnen, hält man sich eng an die oben angegebene Definition, berechnet explizit einen Differenzenquotienten und lässt dann $ \Delta x $ gegen Null gehen. In der Schulmathematik wird dies als „h-Methode“ bezeichnet. Der typische Mathematikanwender vollzieht diese Berechnung nur ein paar wenige Male in seinem Leben nach. Später kennt er die Ableitungen der wichtigsten elementaren Funktionen auswendig, schlägt Ableitungen nicht ganz so geläufiger Funktionen in einem Tabellenwerk (z. B. im Bronstein-Semendjajew oder unserer Tabelle von Ableitungs- und Stammfunktionen) nach und berechnet die Ableitung zusammengesetzter Funktionen mit Hilfe der Ableitungsregeln.

Beispiel für die elementare Berechnung einer Ableitungsfunktion

Gesucht sei die Ableitung von $ f(x)=x^{2}-3x+2 $. Dann berechnet man den Differenzenquotienten als

$ {\begin{aligned}{\frac {\Delta y}{\Delta x}}&={\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}\\&={\frac {{\bigl (}(x_{0}+\Delta x)^{2}-3(x_{0}+\Delta x)+2{\bigr )}-(x_{0}^{2}-3x_{0}+2)}{\Delta x}}\\&={\frac {x_{0}^{2}+2x_{0}\Delta x+\Delta x^{2}-3x_{0}-3\Delta x+2-x_{0}^{2}+3x_{0}-2}{\Delta x}}\\&={\frac {2x_{0}\Delta x+\Delta x^{2}-3\Delta x}{\Delta x}}\\&=2x_{0}+\Delta x-3.\end{aligned}} $

und erhält im Limes $ \Delta x\to 0 $ die Ableitung der Funktion

$ f'(x_{0})=\lim _{\Delta x\to 0}(2x_{0}+\Delta x-3)=2x_{0}-3. $

Beispiel für eine nicht überall differenzierbare Funktion

$ f(x)=|x| $ ist an der Stelle 0 nicht differenzierbar:

Für alle $ x>0 $ gilt nämlich $ f(x)=x $ und damit

$ \lim _{x\searrow 0}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\searrow 0}{\frac {x-0}{x-0}}=1 $.

Für alle $ x<0 $ gilt dagegen $ f(x)=-x $ und folglich

$ \lim _{x\nearrow 0}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\nearrow 0}{\frac {-x-0}{x-0}}=-1 $.

Da der links- und der rechtsseitige Grenzwert nicht übereinstimmen, existiert der Grenzwert nicht. Die Funktion $ f $ ist somit an der betrachteten Stelle nicht differenzierbar. Die Differenzierbarkeit der Funktion an allen anderen Stellen ist dagegen noch immer gegeben.

Es existieren an der Stelle 0 jedoch die rechtsseitige Ableitung

$ f'_{+}(0)=\lim _{x\searrow 0}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\searrow 0}{\frac {x-0}{x-0}}=1 $

und die linksseitige Ableitung

$ f'_{-}(0)=\lim _{x\nearrow 0}{\frac {f(x)-f(0)}{x-0}}=\lim _{x\nearrow 0}{\frac {-x-0}{x-0}}=-1 $.

Betrachtet man den Graphen von $ f $, so kommt man zu der Erkenntnis, dass der Begriff der Differenzierbarkeit anschaulich bedeutet, dass der zugehörige Graph knickfrei verläuft.

Ein typisches Beispiel für nirgends differenzierbare stetige Funktionen, deren Existenz zunächst schwer vorstellbar erscheint, sind fast alle Pfade der brownschen Bewegung. Diese wird zum Beispiel zur Modellierung der Charts von Aktienkursen benutzt.

Beispiel für eine nicht überall stetig differenzierbare Funktion

Eine Funktion heißt stetig differenzierbar, wenn ihre Ableitung stetig ist. Selbst wenn eine Funktion überall differenzierbar ist, muss die Ableitung nicht stetig sein. Zum Beispiel ist die Funktion

$ f(x)={\begin{cases}x^{2}\cos \left({\frac {1}{x}}\right)&x\neq 0\\0&x=0\end{cases}} $

an jeder Stelle, inklusive $ x=0 $, differenzierbar. Die Ableitung, die an der Stelle 0 über den Differenzenquotient bestimmt werden kann,

$ f'(x)={\begin{cases}2x\cos \left({\frac {1}{x}}\right)+\sin \left({\frac {1}{x}}\right)&x\neq 0\\0&x=0\end{cases}} $

ist aber an der Stelle 0 nicht stetig.

Ableitungsregeln

Ableitungen zusammengesetzter Funktionen, z.B. $ \sin(2x) $ oder $ x^{2}\cdot \exp(-x^{2}) $, führt man mit Hilfe von Ableitungsregeln auf die Differentiation elementarer Funktionen zurück (siehe auch: Tabelle von Ableitungs- und Stammfunktionen).

Mit den folgenden Regeln kann man die Ableitung zusammengesetzter Funktionen auf Ableitungen einfacherer Funktionen zurückführen. Seien $ f $, $ g $ und $ h $ (im Definitionsbereich) differenzierbare, reelle Funktionen, $ n $ und $ a $ reelle Zahlen, dann gilt:

Konstante Funktion

$ \left(a\right)'=0 $

Faktorregel

$ (a\cdot f)'=a\cdot f' $

Summenregel

$ \left(g\pm h\right)'=g'\pm h' $

Produktregel

$ (g\cdot h)'=g'\cdot h+g\cdot h' $

Quotientenregel

$ \left({\frac {g}{h}}\right)'={\frac {g'\cdot h-g\cdot h'}{h^{2}}} $

Reziprokenregel

$ \left({\frac {1}{h}}\right)'={\frac {-h'}{h^{2}}} $

Potenzregel

$ \left(x^{n}\right)'=nx^{n-1} $

Kettenregel

$ (g\circ h)'(x)=(g(h(x)))'=g'(h(x))\cdot h'(x) $

Umkehrregel

Ist $ f $ eine an der Stelle $ x_{0} $ differenzierbare, bijektive Funktion mit $ f'(x_{0})\neq 0 $, und ihre Umkehrfunktion $ f^{-1} $ bei $ f(x_{0}) $ differenzierbar, dann gilt:

$ (f^{-1})'(f(x_{0}))={\frac {1}{f'(x_{0})}}. $

Spiegelt man einen Punkt $ P $ des Graphen von $ f $ an der 1. Winkelhalbierenden und erhält damit $ P^{*} $ auf $ f^{-1} $, so ist die Steigung von $ f^{-1} $ in $ P^{*} $ der Kehrwert der Steigung von $ f $ in $ P $

Logarithmische Ableitung

Aus der Kettenregel folgt für die Ableitung des natürlichen Logarithmus einer Funktion $ f $:

$ (\ln(f))'={\frac {f'}{f}} $

Ein Bruch der Form $ f\,'/f $ wird logarithmische Ableitung genannt.

Ableitung der Potenzfunktion

Um $ {\mathsf {}}f(x)=g(x)^{h(x)} $ abzuleiten, erinnert man sich, dass Potenzen mit reellen Exponenten auf dem Umweg über die Exponentialfunktion definiert sind: $ {\mathsf {}}f(x)=\exp {\Big (}h(x)\cdot \ln(g(x)){\Big )} $. Anwendung der Kettenregel und – für die innere Ableitung – der Produktregel ergibt

$ f'(x)=\left(h'(x)\ln(g(x))+h(x){\frac {g'(x)}{g(x)}}\right)g(x)^{h(x)} $.

Leibnizsche Regel

Die Ableitung $ n $-ter Ordnung für ein Produkt aus zwei $ n $-fach differenzierbaren Funktionen $ f $ und $ g $ ergibt sich aus

$ (fg)^{(n)}=\sum _{k=0}^{n}{n \choose k}f^{(k)}g^{(n-k)} $.

Die hier auftretenden Ausdrücke der Form $ {\tbinom {n}{k}} $ sind Binomialkoeffizienten.

Formel von Faà di Bruno

Diese Formel ermöglicht die geschlossene Darstellung der $ n $-ten Ableitung der Komposition zweier $ n $-fach differenzierbarer Funktionen. Sie verallgemeinert die Kettenregel auf höhere Ableitungen.

Der Fundamentalsatz der Analysis

Die wesentliche Leistung von Leibniz war die Erkenntnis, dass Integration und Differentiation zusammenhängen. Diese formulierte er im Hauptsatz der Differential- und Integralrechnung, auch Fundamentalsatz der Analysis genannt. Er besagt:

Ist $ I\subset \mathbb {R} $ ein Intervall, $ f\colon I\to \mathbb {R} $ eine stetige Funktion und $ a\in I $ ein beliebiger Punkt, so ist die Funktion

$ F\colon I\to \mathbb {R} ,\;x\mapsto \int _{a}^{x}f(t)\,\mathrm {d} t $

stetig differenzierbar, und ihre Ableitung ist $ F\,'=f $.

Hiermit ist also eine Anleitung zum Integrieren gegeben: Gesucht ist eine Funktion, deren Ableitung der Integrand ist. Dann gilt:

$ \int _{a}^{b}f(x)\,\mathrm {d} x=F(b)-F(a) $.

Mittelwertsatz der Differentialrechnung

Ein weiterer zentraler Satz der Differentialrechnung ist der Mittelwertsatz, der von Cauchy bewiesen wurde.

Es sei $ f\colon [a,b]\to \mathbb {R} $ eine Funktion, die auf dem abgeschlossenen Intervall $ [a,b] $ (mit $ a<b $) definiert und stetig ist. Außerdem sei die Funktion $ f $ im offenen Intervall $ (a,b) $ differenzierbar. Unter diesen Voraussetzungen gibt es mindestens ein $ x_{0}\in (a,b) $, sodass

$ f'(x_{0})={\frac {f(b)-f(a)}{b-a}} $

gilt.

Mehrfache Ableitungen

Ist die Ableitung einer Funktion $ f $ wiederum differenzierbar, so lässt sich die zweite Ableitung von $ f $ als Ableitung der ersten definieren. Auf dieselbe Weise können dann auch dritte, vierte etc. Ableitungen definiert werden. Eine Funktion kann dementsprechend einfach differenzierbar, zweifach differenzierbar etc. sein.

Die zweite Ableitung kann geometrisch als die Krümmung eines Graphen interpretiert werden. Sie hat zahlreiche physikalische Anwendungen. Zum Beispiel ist die erste Ableitung des Orts $ x(t) $ nach der Zeit $ t $ die Momentangeschwindigkeit, die zweite Ableitung die Beschleunigung. Aus der Physik kommt die Schreibweise $ {\dot {x}}(t) $, (Sprich: $ x $ Punkt), für Ableitungen einer beliebigen Funktion nach der Zeit.

Wenn Politiker sich erfreut über den „Rückgang des Anstiegs der Arbeitslosenzahl“ äußern, dann sprechen sie von der zweiten Ableitung (Änderung des Anstiegs), um die unangenehme Aussage der ersten Ableitung (Anstieg der Arbeitslosenzahl) zu relativieren.

Mehrfache Ableitungen können auf drei verschiedene Weisen geschrieben werden:

$ f''=f^{(2)}={\frac {\mathrm {d} ^{2}f}{\mathrm {d} x^{2}}}, $

$ f'''=f^{(3)}={\frac {\mathrm {d} ^{3}f}{\mathrm {d} x^{3}}},\ldots $

oder im physikalischen Fall (bei einer Ableitung nach der Zeit)

$ {\ddot {x}}(t)={\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}. $

Naheliegenderweise wird die Multi-Apostroph-Schreibweise bei niedrigen, die eine oder andere Zahlen-Schreibweise bei hohen Ableitungen bevorzugt. Für die formale Bezeichnung beliebiger Ableitungen $ f^{(n)} $ legt man außerdem fest, dass $ f^{(1)}=f'\, $ und $ f^{(0)}=f $.

Taylor-Reihen und Glattheit

Ist $ f $ eine ($ n+1 $)-mal stetig differenzierbare Funktion im Intervall $ I $, dann gilt für alle $ a $ und $ x $ aus $ I $ die Darstellung der sogenannten Taylor-Formel:

$ f(x)=T_{n}(x)+R_{n+1}(x) $

mit dem $ n $-ten Taylorpolynom an der Entwicklungsstelle $ a $

$ {\begin{aligned}T_{n}(x)&=\sum _{k=0}^{n}\left({\frac {f^{(k)}(a)}{k!}}(x-a)^{k}\right)\\&=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\dotsb +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}\end{aligned}} $

und dem ($ n+1 $)-ten Restglied

$ R_{n+1}(x)={\frac {1}{n!}}\int _{a}^{x}(x-t)^{n}f^{(n+1)}(t)\mathrm {d} t. $

Eine beliebig oft differenzierbare Funktion wird glatte Funktion genannt. Da sie alle Ableitungen besitzt, kann die oben angegebene Taylor-Formel erweitert werden auf die Taylor-Reihe von $ f $ mit Entwicklungspunkt $ a $

$ {\begin{aligned}&f(a)+f'(a)(x-a)+{\frac {f''(a)}{2}}(x-a)^{2}+\dotsb +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}+\dotsb \\&=\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}.\end{aligned}} $

Es stellt sich allerdings heraus, dass die Existenz aller Ableitungen nicht ergibt, dass $ f $ sich durch die Taylor-Reihe darstellen lässt. Anders ausgedrückt: Jede analytische Funktion ist glatt, aber nicht umgekehrt, wie das im Artikel Taylorreihe gegebene Beispiel einer nicht analytischen glatten Funktion zeigt.

Häufig findet man in mathematischen Betrachtungen den Begriff hinreichend glatt. Hiermit ist gemeint, dass die Funktion so oft differenzierbar ist, wie nötig um den aktuellen Gedankengang durchzuführen.

Anwendungen

Berechnung von Minima und Maxima

Eine der wichtigsten Anwendungen der Differentialrechnung ist die Bestimmung von Extremwerten, meist zur Optimierung von Prozessen. Diese befinden sich unter anderem bei monotonen Funktionen am Rand des Definitionsbereichs, im Allgemeinen jedoch an den Stellen, wo die Ableitung Null ist. Eine Funktion kann einen Maximal- oder Minimalwert haben, ohne dass die Ableitung an dieser Stelle existiert, im folgenden werden jedoch nur zumindest lokal differenzierbare Funktionen betrachtet. Als Beispiel nehmen wir die Polynomfunktion $ f $ mit dem Funktionsterm

$ {f(x)}={\frac {1}{3}}x^{3}-2x^{2}+3x. $

Die Abbildung zeigt den Verlauf der Graphen von $ \,f $, $ \,f' $ und $ \,f'' $ .

Waagerechte Tangenten

Besitzt eine Funktion $ f\colon (a,b)\to \mathbb {R} $ mit $ (a,b)\subset \mathbb {R} $ in einem Punkt $ x_{0}\in (a,b) $ ihren größten Wert, gilt also für alle $ x $ dieses Intervalls $ f(x_{0})\geq f(x) $, und ist $ f $ im Punkt $ x_{0} $ differenzierbar, so kann die Ableitung dort nur gleich null sein: $ f'(x_{0})=0 $. Eine entsprechende Aussage gilt, falls $ f $ in $ x_{0} $ den kleinsten Wert annimmt.

Geometrische Deutung dieses Satzes von Fermat ist, dass der Graph der Funktion in lokalen Extrempunkten eine parallel zur $ x $-Achse verlaufende Tangente, auch waagerechte Tangente genannt, besitzt.

Es ist somit für differenzierbare Funktionen eine notwendige Bedingung für das Vorliegen einer Extremstelle, dass die Ableitung an der betreffenden Stelle den Wert 0 annimmt:

$ f^{\prime }(x_{0})=0 $

Umgekehrt kann daraus, dass die Ableitung an einer Stelle den Wert null hat, noch nicht auf eine Extremstelle geschlossen werden, es könnte auch beispielsweise ein Sattelpunkt vorliegen. Eine Liste verschiedener hinreichender Kriterien, deren Erfüllung sicher auf eine Extremstelle schließen lässt, findet sich im Artikel Extremwert. Diese benutzen meist die zweite oder noch höhere Ableitungen.

Notwendige und hinreichende Bedingung im Beispiel

Im Beispiel ist

$ f'(x)=x^{2}-4\cdot x+3. $

Daraus folgt, dass $ f^{\prime }(x)=0 $ genau für $ x=1 $ und $ x=3 $ gilt. Die Funktionswerte an diesen Stellen sind $ f(1)=4/3 $ und $ f(3)=0 $, d. h. die Kurve hat in den Punkten $ (1\mid 4/3) $ und $ (3\mid 0) $ waagerechte Tangenten, und nur in diesen.

Da die Folge

$ f(0)=0,\quad f(1)={\frac {4}{3}},\quad f(3)=0,\quad f(4)={\frac {4}{3}} $

abwechselnd aus kleinen und großen Werten besteht, muss in diesem Bereich ein Hoch- und ein Tiefpunkt liegen. Nach dem Satz von Fermat hat die Kurve in diesen Punkten eine waagerechte Tangente, es kommen also nur die oben ermittelten Punkte in Frage: Also ist $ (1\mid 4/3) $ ein Hochpunkt und $ (3\mid 0) $ ein Tiefpunkt.

Kurvendiskussion

Mit Hilfe der Ableitungen lassen sich noch weitere Eigenschaften der Funktion analysieren, wie Wendepunkte, Sattelpunkt, Konvexität oder die oben schon angesprochene Monotonie. Die Durchführung dieser Untersuchungen ist Gegenstand der Kurvendiskussion.

Differentialgleichungen

Eine weitere wichtige Anwendung der Differentialrechnung besteht in der mathematischen Modellierung physikalischer Vorgänge. Wachstum, Bewegung oder Kräfte haben alle mit Ableitungen zu tun, ihre formelhafte Beschreibung muss also Differentiale enthalten. Typischerweise führt dies auf Gleichungen, in denen Ableitungen einer unbekannten Funktion auftauchen, eben genau Differentialgleichungen.

Beispielsweise verknüpft das newtonsche Bewegungsgesetz

$ {\vec {F}}(t)=m{\vec {a}}(t)=m{\ddot {\vec {s}}}(t)=m{\frac {\mathrm {d} ^{2}{\vec {s}}(t)}{\mathrm {d} t^{2}}} $

die Beschleunigung $ {\vec {a}} $ eines Körpers mit seiner Masse $ m $ und der auf ihn einwirkenden Kraft $ {\vec {F}} $. Das Grundproblem der Mechanik lautet deshalb, aus einer gegebenen Beschleunigung auf die Ortsfunktion eines Körpers zurückzuschließen. Diese Aufgabe, eine Umkehrung der zweifachen Differentiation, hat die mathematische Gestalt einer Differentialgleichung zweiter Ordnung. Die mathematische Schwierigkeit dieses Problems rührt daher, dass Ort, Geschwindigkeit und Beschleunigung Vektoren sind, die im Allgemeinen nicht in die gleiche Richtung zeigen, und dass die Kraft von der Zeit $ t $ und vom Ort $ {\vec {s}} $ abhängen kann.

Da viele Modelle mehrdimensional sind, sind bei der Formulierung häufig die weiter unten erklärten partiellen Ableitungen sehr wichtig, mit denen sich partielle Differentialgleichungen formulieren lassen. Mathematisch kompakt werden diese mittels Differentialoperatoren beschrieben und analysiert.

Ein Beispiel für angewandte Differentialrechnung

In der Mikroökonomie werden beispielsweise verschiedene Arten von Produktionsfunktionen analysiert, um daraus Erkenntnisse für makroökonomische Zusammenhänge zu gewinnen. Hier ist vor allem das typische Verhalten einer Produktionsfunktion von Interesse: Wie reagiert die abhängige Variable Output $ y $ (produzierte Menge eines Gutes), wenn der Input $ x $ (Produktionsfaktor, z. B. Arbeit oder Kapital) um eine (infinitesimal) kleine Einheit erhöht wird?

Ein Grundtyp einer Produktionsfunktion ist etwa die neoklassische Produktionsfunktion. Sie zeichnet sich dadurch aus, dass der Output bei jedem zusätzlichen Input steigt, dass aber die Zuwächse abnehmend sind. Es sei beispielsweise für einen Betrieb die Produktionsfunktion

$ y=f(x)={\sqrt {4x-400}}\ \mathrm {f{\ddot {u}}r} \ x\geq 100 $

maßgebend. Die erste Ableitung dieser Funktion ergibt unter Anwendung der Kettenregel

$ {\frac {\mathrm {d} y}{\mathrm {d} x}}={\frac {1}{2}}({4x-400})^{-{\frac {1}{2}}}\cdot 4={\frac {2}{\sqrt {4x-400}}} $.

Da der Wurzelausdruck der ersten Ableitung nur positiv werden kann, sieht man, dass der Ertrag bei jedem zusätzlichen Input steigt. Die zweite Ableitung ergibt

$ {\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}=2\left(-{\frac {1}{2}}\right)({4x-400})^{-{\frac {3}{2}}}\cdot 4=-{\frac {4}{\sqrt {(4x-400)^{3}}}} $.

Sie wird für alle Inputs negativ, also fallen die Zuwachsraten. Man könnte also sagen, dass bei steigendem Input der Output unterproportional steigt. Die relative Änderung des Outputs im Verhältnis zu einer relativen Änderung des Inputs ist hier durch die Elastizität $ \varepsilon _{y,x}={\frac {\mathrm {d} y}{\mathrm {d} x}}\cdot {\frac {x}{y}} $ gegeben.

Differentialrechnung als Kalkül

Neben der Bestimmung der Steigung von Funktionen ist die Differentialrechnung durch ihren Kalkül ein wesentliches Hilfsmittel bei der Termumformung. Hierbei löst man sich von jeglichem Zusammenhang mit der ursprünglichen Bedeutung der Ableitung als Anstieg. Hat man zwei Terme als gleich erkannt, lassen sich durch Differentiation daraus weitere (gesuchte) Identitäten gewinnen. Ein Beispiel mag dies verdeutlichen:

Aus der Teleskopsumme:

$ (x-1)\sum _{k=0}^{n}x^{k}=x^{n+1}-1 $

soll

$ (x-1)^{2}\sum _{k=1}^{n}kx^{k-1}=nx^{n+1}-(n+1)x^{n}+1 $

möglichst einfach gewonnen werden. Dies gelingt durch Differentiation mit Hilfe der Quotientenregel:

$ \sum _{k=1}^{n}kx^{k-1}={\frac {\mathrm {d} }{\mathrm {d} x}}\sum _{k=0}^{n}x^{k}={\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {x^{n+1}-1}{x-1}}={\frac {(n+1)x^{n}(x-1)-(x^{n+1}-1)}{(x-1)^{2}}}={\frac {nx^{n+1}-(n+1)x^{n}+1}{(x-1)^{2}}} $

Alternativ ergibt sich die Identität auch durch Ausmultiplizieren und anschließendes dreifaches Teleskopieren, was aber nicht so einfach zu durchschauen ist.

Komplexe Differenzierbarkeit

Bisher wurde nur von reellen Funktionen gesprochen. Für Differenzierbarkeit von Funktionen mit komplexen Argumenten wird einfach die Definition mit der Linearisierung verwandt. Hier ist die Bedingung viel einschränkender als im reellen: So ist beispielsweise die Betragsfunktion nirgendwo komplex differenzierbar. Gleichzeitig ist jede in einer Umgebung einmal komplex differenzierbare Funktion automatisch beliebig oft differenzierbar, es existieren also alle höheren Ableitungen.

Ableitungen von mehrdimensionalen Funktionen

Alle vorherigen Ausführungen legten eine Funktion in einer Variablen (also mit einer reellen oder komplexen Zahl als Argument) zugrunde. Funktionen, die Vektoren auf Vektoren oder Vektoren auf Zahlen abbilden, können ebenfalls eine Ableitung haben. Allerdings ist eine Tangente an den Funktionsgraph in diesen Fällen nicht mehr eindeutig bestimmt, da es viele verschiedene Richtungen gibt. Hier ist also eine Erweiterung des bisherigen Ableitungsbegriffs notwendig.

Partielle Ableitungen

→ Hauptartikel: Partielle Ableitung

Wir betrachten zunächst eine Funktion, die von $ \mathbb {R} ^{n}\to \mathbb {R} $ geht. Ein Beispiel ist die Temperaturfunktion: In Abhängigkeit vom Ort wird die Temperatur im Zimmer gemessen, um zu beurteilen, wie effektiv die Heizung ist. Wird das Thermometer in eine bestimmte Richtung bewegt, ist eine Veränderung der Temperatur festzustellen. Dies entspricht der so genannten Richtungsableitung. Die Richtungsableitungen in spezielle Richtungen, nämlich die der Koordinatenachsen, nennt man die partiellen Ableitungen.

Insgesamt lassen sich für eine Funktion in $ n $ Variablen insgesamt $ n $ partielle Ableitungen errechnen:

$ {\frac {\partial f(x_{1},\dots ,x_{n})}{\partial x_{i}}} $

$ =\lim _{\Delta x_{i}\to 0}{\frac {f(x_{1},\dots ,x_{i}+\Delta x_{i},\dots ,x_{n})-f(x_{1},\dots ,x_{i},\dots ,x_{n})}{\Delta x_{i}}};\quad i\in \{1,\dots ,n\} $

Die einzelnen partiellen Ableitungen einer Funktion lassen sich auch gebündelt als Gradient oder Nablavektor anschreiben. Partielle Ableitungen können wieder differenzierbar sein und lassen sich dann in der so genannten Hesse-Matrix anordnen. Analog zum eindimensionalen Fall sind die Kandidaten für Extremstellen da, wo die Ableitung Null ist, also der Gradient verschwindet. Ebenfalls analog benutzt man die zweite Ableitung, also die Hesse-Matrix, zur Bestimmung des exakt vorliegenden Falles. Im Gegensatz zum eindimensionalen ist allerdings die Formenvielfalt in diesem Falle größer. Mittels einer Hauptachsentransformation der durch eine mehrdimensionale Taylor-Entwicklung im betrachteten Punkt gegebenen quadratischen Form lassen sich die verschiedenen Fälle klassifizieren.

Implizite Differentiation

→ Hauptartikel: Implizite Differentiation

Ist eine Funktion $ x\mapsto y(x) $ durch eine implizite Gleichung $ F\left(x,y(x)\right)=0 $ gegeben, so folgt aus der verallgemeinerten Kettenregel, die für Funktionen mehrerer Variablen gilt

$ F_{x}+F_{y}y'=0. $

Für die Ableitung der Funktion $ y $ ergibt sich daher

$ y'=-{\frac {F_{x}}{F_{y}}} $ mit $ F_{x}={\frac {\partial F}{\partial x}},F_{y}={\frac {\partial F}{\partial y}};F_{y}\neq 0. $

Totale Differenzierbarkeit

→ Weiterführender Artikel: Totale Differenzierbarkeit

Eine Funktion $ f\colon U\subset \mathbb {R} ^{n}\to \mathbb {R} ^{m} $, wobei $ U $ eine offene Menge ist, heißt in einem Punkt $ x_{0}\in U $ total differenzierbar (oder auch nur differenzierbar), falls eine lineare Abbildung $ L\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m} $ existiert, so dass

$ \lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})-Lh}{\|h\|}}=0 $ gilt.

Für den eindimensionalen Fall stimmt diese Definition mit der oben angegebenen überein. Die lineare Abbildung $ L $ ist bei Existenz eindeutig bestimmt, ist also insbesondere unabhängig von der Wahl äquivalenter Normen. Die Tangente wird also durch die lokale Linearisierung der Funktion abstrahiert. Die Matrixdarstellung der ersten Ableitung von $ f $ nennt man Jacobi-Matrix. Es handelt sich um eine $ m\times n $-Matrix. Für $ m=1 $ erhält man den oben beschriebenen Gradienten.

Zwischen den partiellen Ableitungen und der totalen Ableitung besteht folgender Zusammenhang: Existiert in einem Punkt die totale Ableitung, so existieren dort auch alle partiellen Ableitungen. In diesem Fall stimmen die partiellen Ableitungen mit den Koeffizienten der Jacobi-Matrix überein. Umgekehrt folgt aus der Existenz der partiellen Ableitungen in einem Punkt $ x_{0} $ nicht zwingend die totale Differenzierbarkeit, ja nicht einmal die Stetigkeit. Sind die partiellen Ableitungen jedoch zusätzlich in einer Umgebung von $ x_{0} $ stetig, dann ist die Funktion in $ x_{0} $ auch total differenzierbar.

Wichtige Sätze

• Satz von Schwarz: Die Differentiationsreihenfolge ist bei der Berechnung von partiellen Ableitungen höherer Ordnung unerheblich, wenn alle partiellen Ableitungen bis zu dieser Ordnung (einschließlich) stetig sind.
• Satz von der impliziten Funktion: Funktionsgleichungen sind lösbar, falls die Jacobi-Matrix bezüglich bestimmter Variablen lokal invertierbar ist.

Verallgemeinerungen und verwandte Gebiete

• In vielen Anwendungen ist es wünschenswert, Ableitungen auch für stetige oder sogar unstetige Funktionen bilden zu können. So kann beispielsweise eine sich am Strand brechende Welle durch eine partielle Differentialgleichung modelliert werden, die Funktion der Höhe der Welle ist aber noch nicht einmal stetig. Zu diesem Zweck verallgemeinerte man Mitte des 20. Jahrhunderts den Ableitungsbegriff auf den Raum der Distributionen und definierte dort eine schwache Ableitung. Eng verbunden damit ist der Begriff des Sobolew-Raums.
• In der Differentialgeometrie werden gekrümmte Flächen untersucht. Hierzu wird der Begriff der Differentialform benötigt.
• Der Begriff der Ableitung als Linearisierung lässt sich analog auf Funktionen $ f(x) $ zwischen zwei normierbaren topologischen Vektorräumen $ X $ und $ Y $ übertragen (s. Hauptartikel: Fréchet-Ableitung, Gâteaux-Differential, Lorch-Ableitung): $ f $ heißt dann in $ \xi $ Fréchet-differenzierbar, wenn ein stetiger linearer Operator $ L_{\xi }\in {\mathcal {L}}(X,Y) $ existiert, so dass

$ \lim _{h\to 0}{\frac {\|f(\xi +h)-f(\xi )-L_{\xi }h\|}{\|h\|}}=0 $.

• Eine Übertragung des Begriffes der Ableitung auf andere Ringe als $ \mathbb {R} $ und $ \mathbb {C} $ (und Algebren darüber) ist die Derivation.
• Die Differenzenrechnung überträgt die Differentialrechnung auf Reihen.

Literatur

Schulbücher

• Differentialrechnung ist ein zentraler Unterrichtsgegenstand in der Sekundarstufe II und wird somit in allen Mathematik-Lehrbüchern dieser Stufe behandelt.

Lehrbücher für Studenten der Mathematik und benachbarter Fächer

• Henri Cartan: Differentialrechnung. Bibliographisches Institut, Mannheim 1974. ISBN 3-411-01442-3
• Henri Cartan: Differentialformen. Bibliographisches Institut, Mannheim 1974. ISBN 3-411-01443-1
• Henri Cartan: Elementare Theorien der Analytischen Funktionen einer und mehrerer Komplexen Veränderlichen. Bibliographisches Institut, Mannheim 1966, 1981. ISBN 3-411-00112-7
• Richard Courant: Vorlesungen über Differential- und Integralrechnung. 2 Bde. Springer 1928, ⁴1971. ISBN 3-540-02956-7
• Jean Dieudonné: Grundzüge der modernen Analysis. Bd. 1. Vieweg, Braunschweig 1972. ISBN 3-528-18290-3
• Gregor M. Fichtenholz: Differential- und Integralrechnung I-III Verlag Harri Deutsch, Frankfurt am Main, 1990-2004. ISBN 978-3-8171-1418-4 (kompletter Satz)
• Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg, Braunschweig ⁷2004. ISBN 3-528-67224-2
• Otto Forster: Analysis 2. Differentialrechnung im Rⁿ. Gewöhnliche Differentialgleichungen. Vieweg, Braunschweig ⁶2005. ISBN 3-528-47231-6
• Konrad Königsberger: Analysis. 2 Bde. Springer, Berlin 2004, ISBN 3-540-41282-4
• Wladimir I. Smirnow: Lehrgang der höheren Mathematik (Teil 1-5). Verlag Harri Deutsch, Frankfurt am Main, 1995-2004. ISBN 978-3-8171-1419-1 (kompletter Satz)
• Steffen Timmann: Repetitorium der Analysis. 2 Bde. Binomi, Springe 1993. ISBN 3-923923-50-3, ISBN 3-923923-52-X

Lehrbücher für Studenten mit Nebenfach/Grundlagenfach Mathematik

• Rainer Ansorge, Hans Joachim Oberle: Mathematik für Ingenieure. Bd. 1. Akademie-Verlag, Berlin 1994, ³2000. ISBN 3-527-40309-4
• Günter Bärwolff (unter Mitarbeit von G. Seifert): Höhere Mathematik für Naturwissenschaftler und Ingenieure. Elsevier Spektrum Akademischer Verlag, München 2006. ISBN 3-8274-1688-4
• Lothar Papula: Mathematik für Naturwissenschaftler und Ingenieure. Bd. 1. Vieweg, Wiesbaden 2004. ISBN 3-528-44355-3
• Klaus Weltner: Mathematik für Physiker. Bd. 1. Springer, Berlin 2006. ISBN 3-540-29842-8
• Peter Dörsam: Mathematik anschaulich dargestellt für Studierende der Wirtschaftswissenschaften. PD-Verlag, Heidenau 2010 (15. Auflage). ISBN 978-3-86707-015-7

Weblinks

• Tool zur Bestimmung von Ableitungen beliebiger Funktionen mit einer oder mehreren Variablen mit Rechenweg (deutsch; benötigt JavaScript)
• Online-Rechner zum Ableiten von Funktionen mit Rechenweg und Erklärungen (deutsch)
• Tool zur Bestimmung von Ableitungen und Stammfunktionen von Funktionen mit einer Variablen (englisch)
• Grundidee des Differenzierens – Filmclip
• Anschauliche Erklärung von Ableitungen

Dieser Artikel wurde am 19. Februar 2005 in dieser Version in die Liste der exzellenten Artikel aufgenommen.